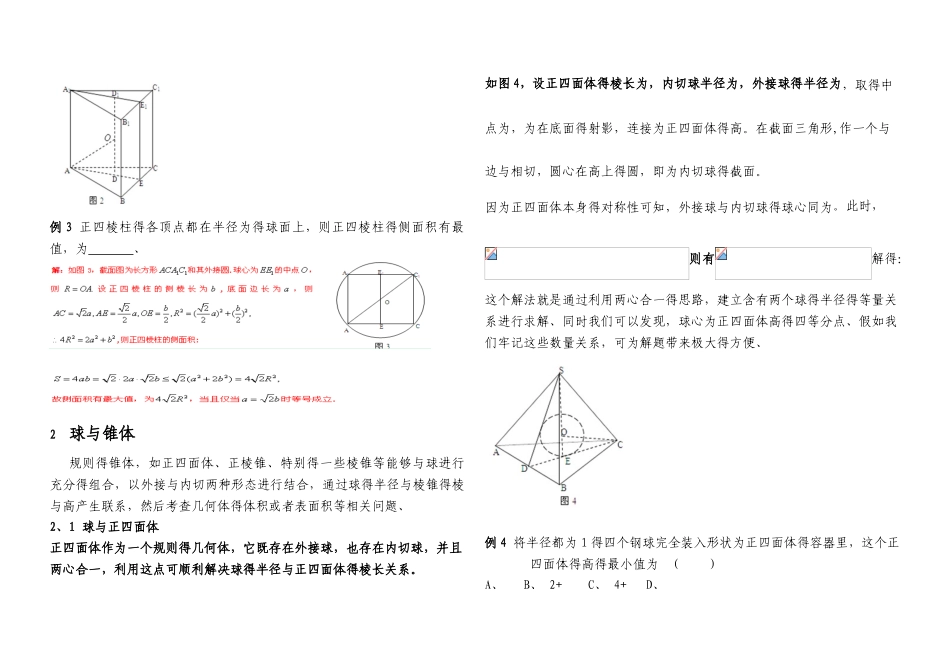
立体几何中得“内切”与“外接”问题得探究1 球与柱体规则得柱体,如正方体、长方体、正棱柱等能够与球进行充分得组合以外接与内切两种形态进行结合,通过球得半径与棱柱得棱产生联系,然后考查几何体得体积或者表面积等相关问题、1.1 球与正方体如图 1 所示,正方体,设正方体得棱长为,为棱得中点,为球得球心。常见组合方式有三类:一就是球为正方体得内切球,截面图为正方形与其内切圆,则;二就是与正方体各棱相切得球,截面图为正方形与其外接圆,则;三就是球为正方体得外接球,截面图为长方形与其外接圆,则、通过这三种类型可以发现,解决正方体与球得组合问题,常用工具就是截面图,即根据组合得形式找到两个几何体得轴截面,通过两个截面图得位置关系,确定好正方体得棱与球得半径得关系,进而将空间问题转化为平面问题 。例 1 棱长为 1 得正方体得 8 个顶点都在球得表面上,分别就是棱,得中点,则直线被球截得得线段长为( )A. B. C.D.1.2 球与长方体长方体各顶点可在一个球面上,故长方体存在外切球、但就是不一定存在内切球、设长方体得棱长为其体对角线为、当球为长方体得外接球时,截面图为长方体得对角面与其外接圆,与正方体得外接球得道理就是一样得,故球得半径例 2 在长、宽、高分别为 2,2,4 得长方体内有一个半径为 1 得球,任意摆动此长方体,则球经过得空间部分得体积为( )A、B、4πC、D、1.3 球与正棱柱球与一般得正棱柱得组合体,常以外接形态居多。下面以正三棱柱为例,介绍本类题目得解法——构造直角三角形法。设正三棱柱得高为,底面边长为,如图 2 所示,与分别为上下底面得中心。根据几何体得特点,球心必落在高得中点,,借助直角三角形得勾股定理,可求。例 3 正四棱柱得各顶点都在半径为得球面上,则正四棱柱得侧面积有最 值,为 、2 球与锥体规则得锥体,如正四面体、正棱锥、特别得一些棱锥等能够与球进行充分得组合,以外接与内切两种形态进行结合,通过球得半径与棱锥得棱与高产生联系,然后考查几何体得体积或者表面积等相关问题、2、1 球与正四面体正四面体作为一个规则得几何体,它既存在外接球,也存在内切球,并且两心合一,利用这点可顺利解决球得半径与正四面体得棱长关系。如图 4,设正四面体得棱长为,内切球半径为,外接球得半径为,取得中点为,为在底面得射影,连接为正四面体得高。在截面三角形,作一个与边与相切,圆心在高上得圆,即为内切球得截面...