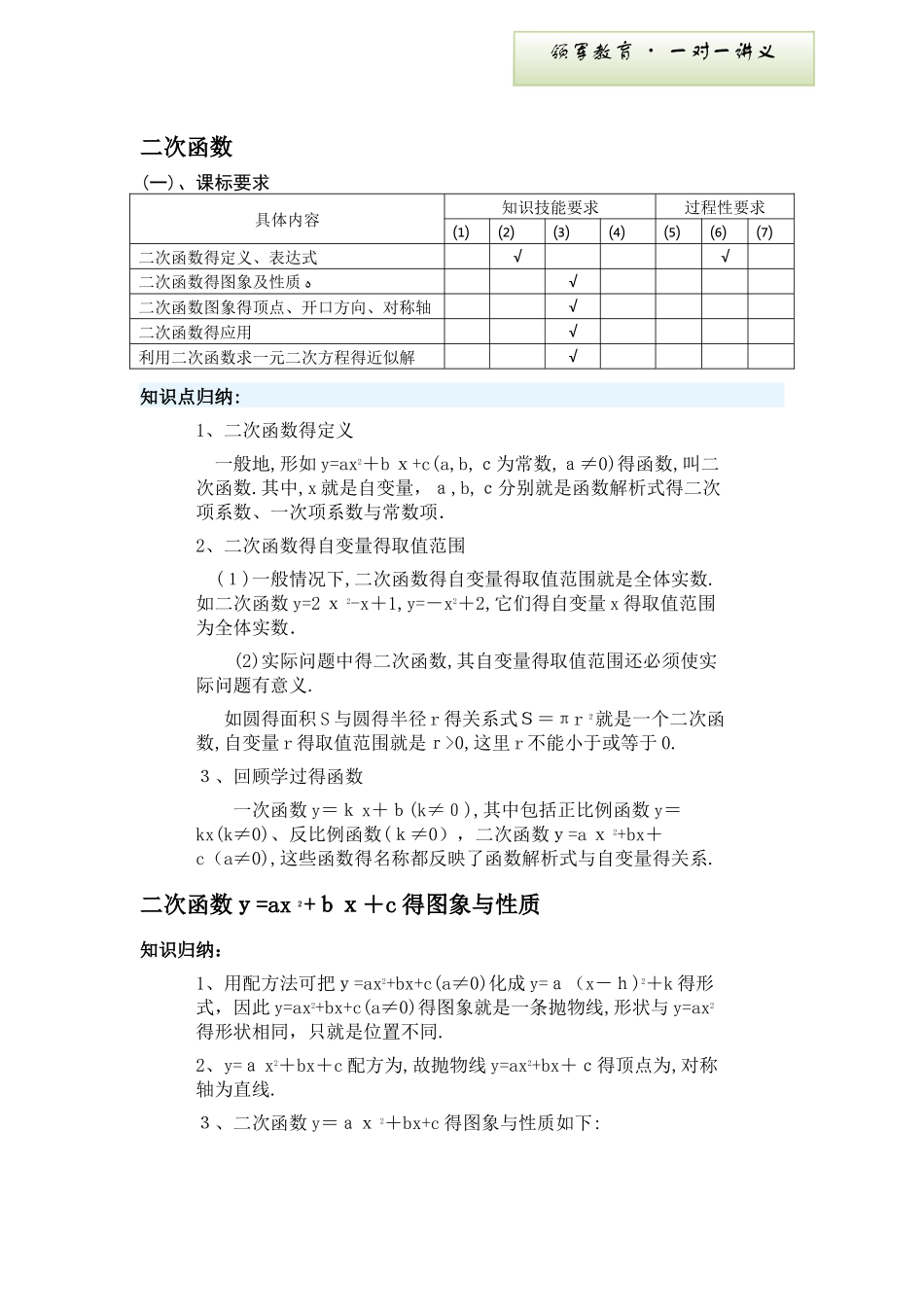
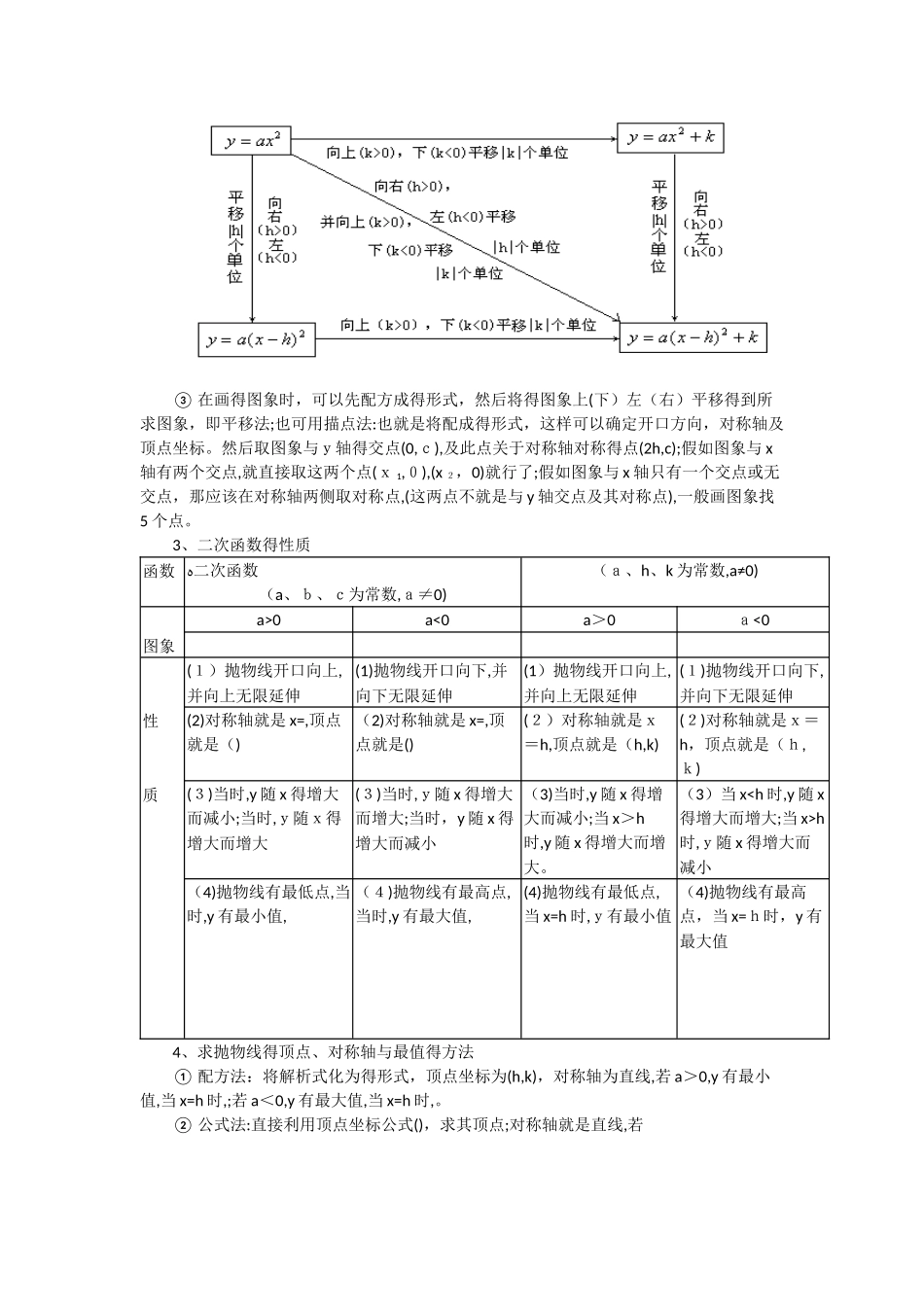
二次函数(一)、课标要求具体内容知识技能要求过程性要求⑴⑵⑶⑷⑸⑹⑺二次函数得定义、表达式√√二次函数得图象及性质ﻩ√二次函数图象得顶点、开口方向、对称轴√二次函数得应用√利用二次函数求一元二次方程得近似解√知识点归纳:1、二次函数得定义 一般地,形如 y=ax2+b x+c(a,b,c为常数,a≠0)得函数,叫二次函数.其中,x 就是自变量,a,b,c分别就是函数解析式得二次项系数、一次项系数与常数项.2、二次函数得自变量得取值范围 (1)一般情况下,二次函数得自变量得取值范围就是全体实数.如二次函数 y=2 x 2-x+1,y=-x2+2,它们得自变量 x 得取值范围为全体实数. (2)实际问题中得二次函数,其自变量得取值范围还必须使实际问题有意义. 如圆得面积 S 与圆得半径 r 得关系式S=πr 2就是一个二次函数,自变量 r 得取值范围就是r>0,这里 r 不能小于或等于 0.3、回顾学过得函数 一次函数 y=k x+b(k≠0),其中包括正比例函数 y=kx(k≠0)、反比例函数(k≠0),二次函数y=a x 2+bx+c(a≠0),这些函数得名称都反映了函数解析式与自变量得关系.二次函数y=ax 2+bx+c 得图象与性质知识归纳:1、用配方法可把y=ax2+bx+c(a≠0)化成 y=a(x-h)2+k 得形式,因此 y=ax2+bx+c(a≠0)得图象就是一条抛物线,形状与 y=ax2得形状相同,只就是位置不同.2、y=a x2+bx+c 配方为,故抛物线 y=ax2+bx+c得顶点为,对称轴为直线.3、二次函数 y=ax 2+bx+c 得图象与性质如下:领军教育 · 一对一讲义 ①当 a>0 时,抛物线 y=ax2+b x+c得开口向上,时,y 随x得增大而减小;时,y 随 x 得增大而增大;时,y 有最小值,则抛物线得顶点就是其最低点.② 当a<0 时,抛物线 y=a x2+bx+c 得开口向下,时,y 随 x 得增大而增大;时,y 随 x 得增大而减小;时,y有最大值,则抛物线得顶点就是其最高点.二次函数y=a(x-h)2+k得图象与性质知识归纳:ﻩ1、二次函数 y=a(x-h)2+k(a≠0)得图象就是一条抛物线,它得形状与 y=a x2(a≠0)得形状相同,只就是位置不同.抛物线y=a(x-h)2+k 得顶点就是(h,k),对称轴就是直线 x=h.2、二次函数 y=a(x-h)2+k(a≠0)得性质如下: 当a>0 时,若 xh,则 y 随 x得增大而增大;当 x=h 时,y 有最小值 k; 当a<0 时,若 x<h,则 y 随x得增大而增大;若x>h,则 y 随x得增大...