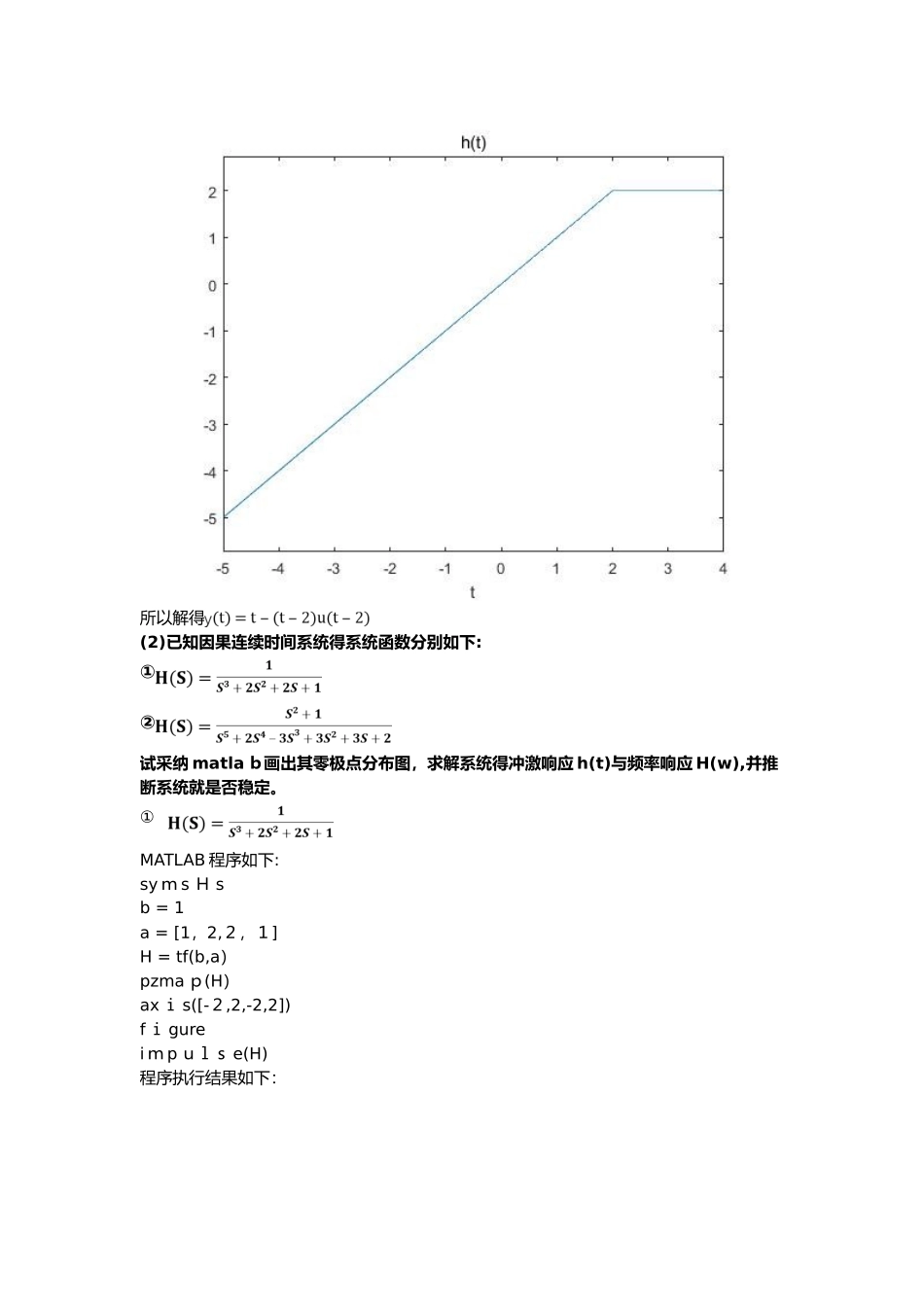
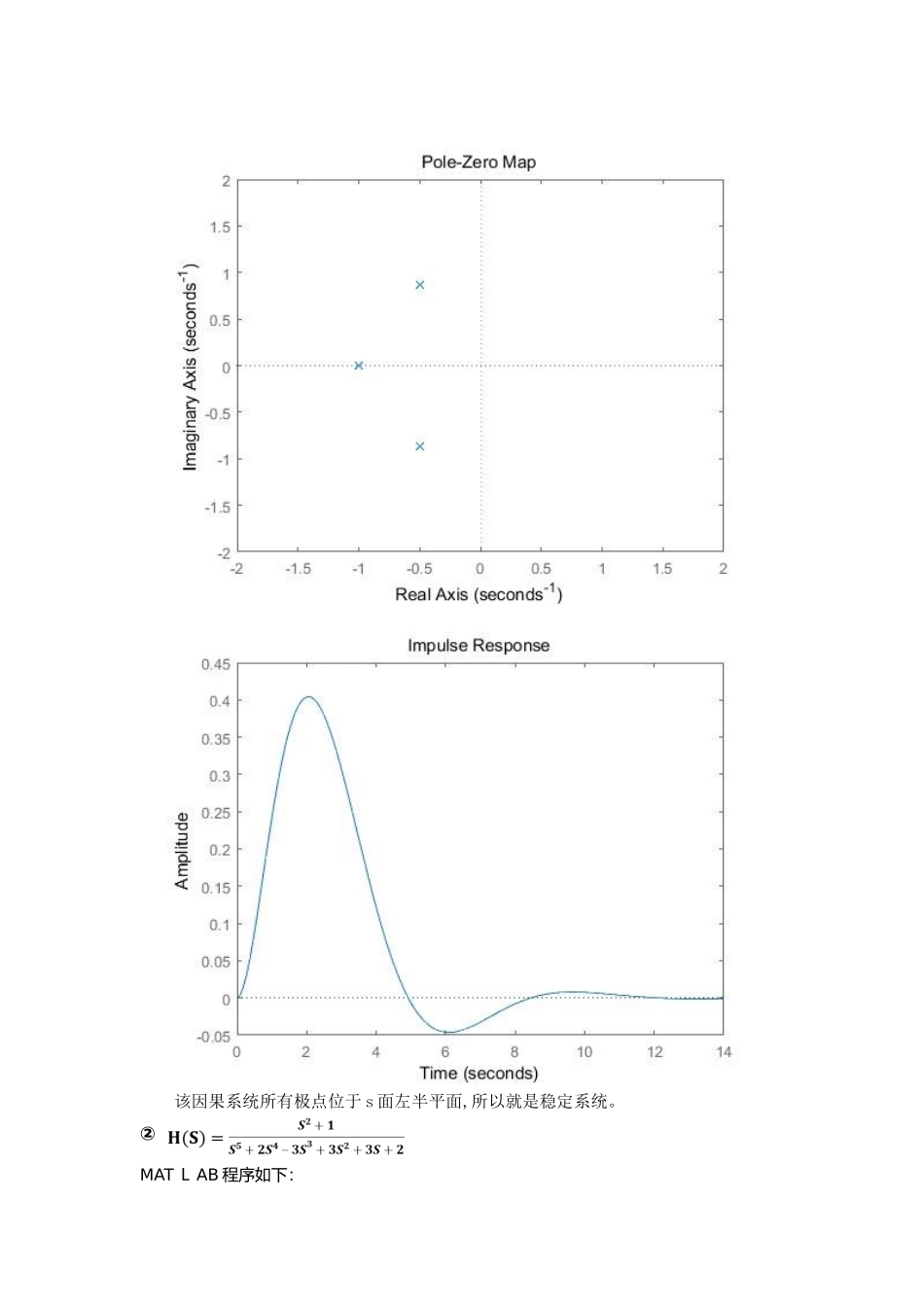
一,实验目得针对拉普拉斯变换及其反变换,了解定义、并掌握 matlab 实现方法;掌握连续时间系统函数得定义与复频域分析方法;利用 M ATLAB 加深掌握系统零极点与系统分布。二,实验原理1、拉普拉斯变换调用la place 与 ila p lace 函数表示拉氏变换与拉氏反变换:L=lapl a ce(F)符号表达式 F 得拉氏变换,F 中时间变量为 t,返回变量为 s 得结果表达式。L=laplace(F,t)用 t 替换结果中得变量 s。F=il ap lace(L)以 s 为变量得符号表达式 L 得拉氏反变换,返回时间变量为 t 得结果表达式。F=i l a place(L,x)用x替换结果中得变量 t。2、连续时间系统得系统函数3、连续时间系统得零极点分析求多项式得根可以通过r oots 来实现:r=roots(c) c 为多项式得系数向量,返回值 r 为多项式得根向量。绘制系统函数得零极点分布图,可调用 pzm a p 函数:Pzma p(sys)绘出由系统模型s ys 描述得系统得零极点分布图。[p,z]=pz m ap(sys)返回极点与零点,不绘出分布图。三,实验内容(1)已知系统得冲激响应 h(t)=u(t)-u(t-2),输入信号x(t)=u(t),试采纳复频域得方法求解系统得响应,编写M ATL A B 程序实现。MA T LAB 程序如下:sy ms t h x y H X h = he avi side(t) - he a v i side(t - 2)x = h e avisi d e(t)H = la pl ac e(h)X = l a p la c e(x)Y = X*Hy = il a place(Y)disp(y)ezplo t(y,[-5,4])title('h(t)')程序执行结果如下:所以解得(2)已知因果连续时间系统得系统函数分别如下:①②试采纳 matla b画出其零极点分布图,求解系统得冲激响应 h(t)与频率响应 H(w),并推断系统就是否稳定。①MATLAB 程序如下:sy m s H sb = 1a = [1,2,2,1]H = tf(b,a)pzma p(H)ax i s([-2,2,-2,2])f i gurei m p uls e(H)程序执行结果如下:该因果系统所有极点位于 s 面左半平面,所以就是稳定系统。②MAT L AB 程序如下: b = [1,0,1]a=[1,2,-3,3,3,2]H = tf(b,a)f i g urepzma p(H)a xis([-3、5,3、5,-3、5,3、5])f i gurei mp u l s e(H)程序执行结果如下:该因果系统得极点不全位于 S 平面得左半平面,所以系统就是不稳定系统。(3)已知连续时间系统函数得极点位置分别如下所示:试用M ATLA B绘制下述 6...