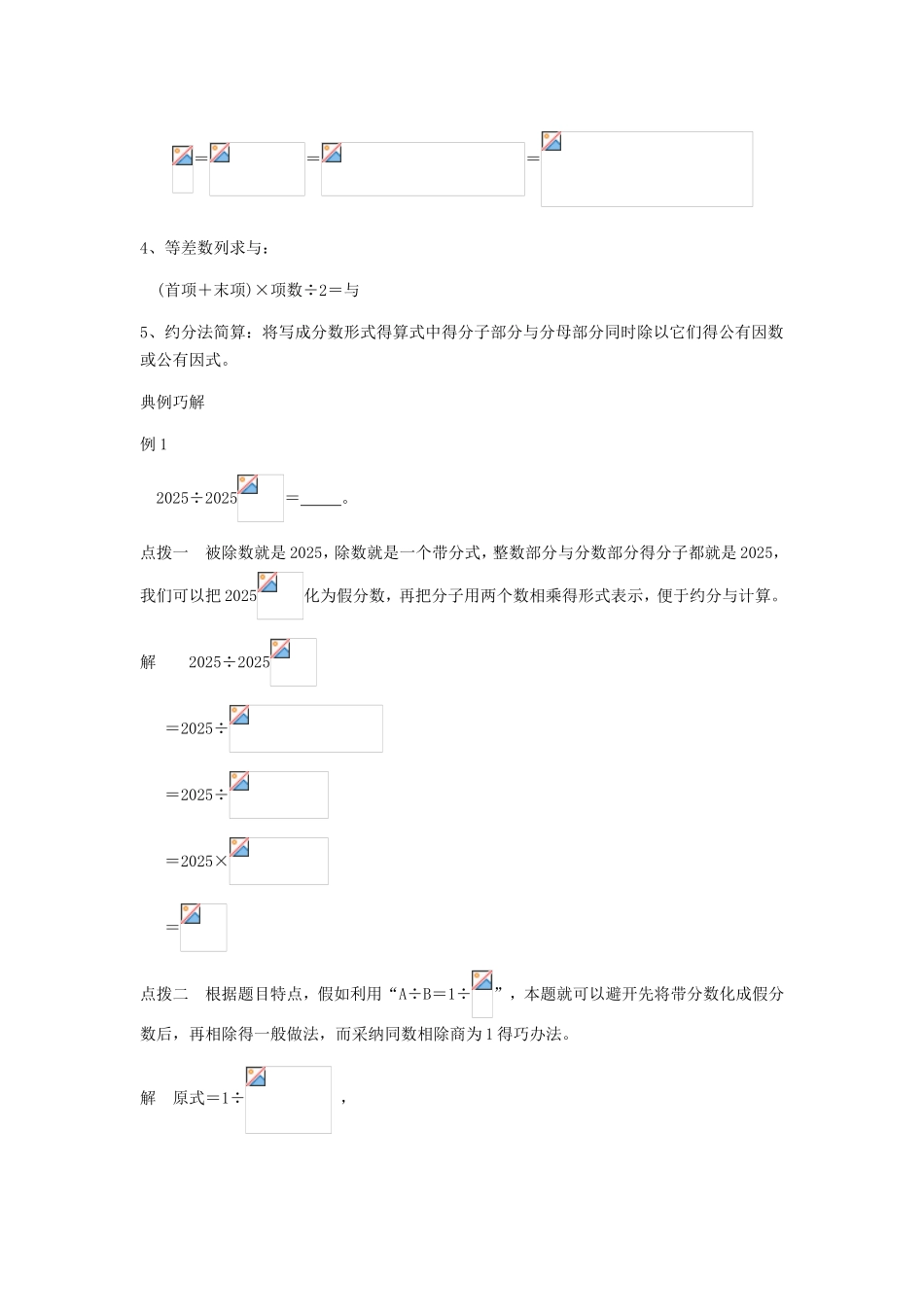
速算与巧算 数学竞赛中,都有一定数量得计算题。计算题一般可以分为两类:一类就是基础题,主要考查对基础知识理解与掌握得程度;另一类则就是综合性较强与灵活性较大得题目,主要考查灵活、综合运用知识得能力,一般分值在 10 分到 20 分之间。这就要求有扎实得基础知识与熟练得技巧。1、速算与巧算主要就是运用定律:加法得交换律、结合律,减法得性质,乘法得交换律、结合律与乘法对加法得分配律,除法得性质等。2、除法运算规律: (1)A÷B=1÷ (2)a÷b±c÷b=(a±c)÷b3、拆项法:(1) (2) (3) (4) (5)(6)将分拆成两个分数单位与得方法:先找出 A 得两个约数 a1与 a2,然后分子、分母分别乘以(a1+a2),再拆分,最后进行约分。 ===4、等差数列求与:(首项+末项)×项数÷2=与5、约分法简算:将写成分数形式得算式中得分子部分与分母部分同时除以它们得公有因数或公有因式。典例巧解例 1 2025÷2025= 。点拨一 被除数就是 2025,除数就是一个带分式,整数部分与分数部分得分子都就是 2025,我们可以把 2025化为假分数,再把分子用两个数相乘得形式表示,便于约分与计算。解 2025÷2025 =2025÷ =2025÷ =2025× = 点拨二 根据题目特点,假如利用“A÷B=1÷”,本题就可以避开先将带分数化成假分数后,再相除得一般做法,而采纳同数相除商为 1 得巧办法。解 原式=1÷ , =1÷1 =说明 本题“巧”在倒数概念得运用。例 2 (第五届“希望杯”邀请赛试题) = 。点拨 此题分子可化简去括号变成因数乘积得形式,再约分化简,分母可通过凑整变形化简,问题易解。解 ==例 3 计算:。点拨 初瞧题目,分子、分母都就是一组有一定规律得数列,可以先分别求出与,再求它们得商,但事实上,求出与得结果就是不易做到得。再认真观察分子、分母,可以发现对应项之间存在一定得规律: 3÷1=×=2,5÷2=×=2,7÷3=×=2,…,55÷27=×=2,57÷28=2。 这说明分母得总与正好就是分子总与得 2 倍,问题易解。解 = =说明 在计算 55÷27时,假如不用常规得办法,先将带分数转化为假分数,而就是利用题目中得数据,再经过转化,逆向运用乘法分配律,就更简便。如: 被除数=55×29+27=54×29+(29+27)=2×(27×29)+2×28=2×(27×29+28), 除数=27×29+28,仍然可以瞧出被除数正好就是除数得 2 倍。例 4 计算: 。点拨 观察题目可知,要求计算得繁分数得分子与分母...