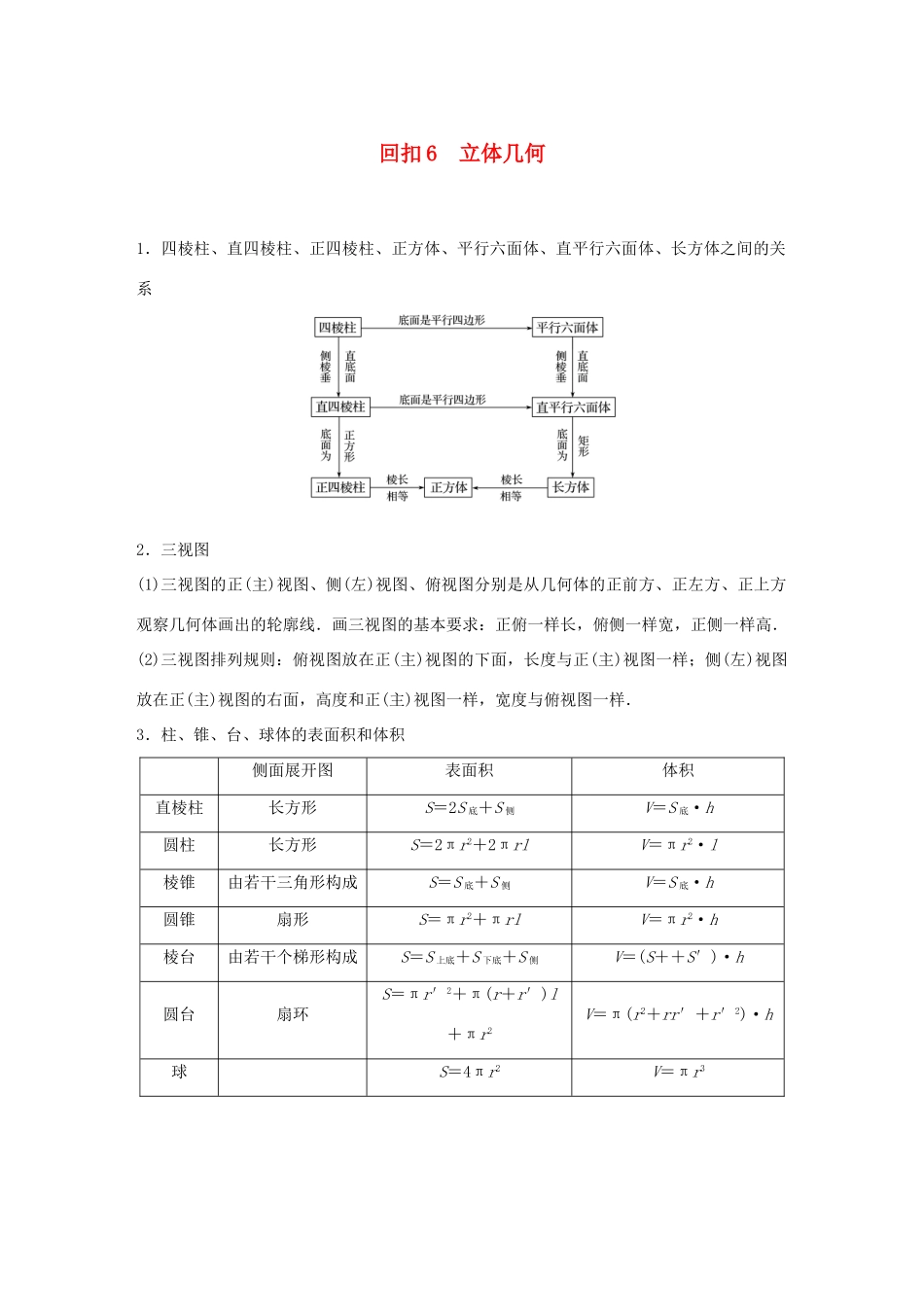
回扣 6 立体几何1.四棱柱、直四棱柱、正四棱柱、正方体、平行六面体、直平行六面体、长方体之间的关系2.三视图(1)三视图的正(主)视图、侧(左)视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线.画三视图的基本要求:正俯一样长,俯侧一样宽,正侧一样高.(2)三视图排列规则:俯视图放在正(主)视图的下面,长度与正(主)视图一样;侧(左)视图放在正(主)视图的右面,高度和正(主)视图一样,宽度与俯视图一样.3.柱、锥、台、球体的表面积和体积侧面展开图表面积体积直棱柱长方形S=2S 底+S 侧V=S 底·h圆柱长方形S=2πr2+2πrlV=πr2·l棱锥由若干三角形构成S=S 底+S 侧V=S 底·h圆锥扇形S=πr2+πrlV=πr2·h棱台由若干个梯形构成S=S 上底+S 下底+S 侧V=(S++S′)·h圆台扇环S=πr′2+π(r+r′)l+πr2V=π(r2+rr′+r′2)·h球S=4πr2V=πr34.平行、垂直关系的转化示意图(1)(2)两个结论①⇒a∥b,②⇒b⊥α.1.混淆“点 A 在直线 a 上”与“直线 a 在平面 α 内”的数学符号关系,应表示为A∈a,a⊂α.2.在由三视图还原为空间几何体的实际形状时,根据三视图的规则,空间几何体的可见轮廓线在三视图中为实线,不可见轮廓线为虚线.在还原空间几何体实际形状时一般是以正(主)视图和俯视图为主.3.易混淆几何体的表面积与侧面积的区别,几何体的表面积是几何体的侧面积与所有底面面积之和,不能漏掉几何体的底面积;求锥体体积时,易漏掉体积公式中的系数.4.不清楚空间线面平行与垂直关系中的判定定理和性质定理,忽视判定定理和性质定理中的条件,导致判断出错.如由 α⊥β,α∩β=l,m⊥l,易误得出 m⊥β 的结论,就是因为忽视面面垂直的性质定理中 m⊂α 的限制条件.5.注意图形的翻折与展开前后变与不变的量以及位置关系.对照前后图形,弄清楚变与不变的元素后,再立足于不变的元素的位置关系与数量关系去探求变化后的元素在空间中的位置与数量关系.6.几种角的范围两条异面直线所成的角:0°<α≤90°;直线与平面所成的角:0°≤α≤90°.1.已知某几何体的三视图如图所示,则该几何体的表面积为( )A.16B.26C.32D.20+答案 C解析 由三视图知,该几何体的直观图如图,其表面积为 S=×3×4+×3×4+×5×4+×5×4=32,故选 C.2.直三棱柱 ABC—A1B1C1的直观图及三视图如图所示,D 为 AC 的中点,则下列命题中是假命题的是( ) A.AB1∥...