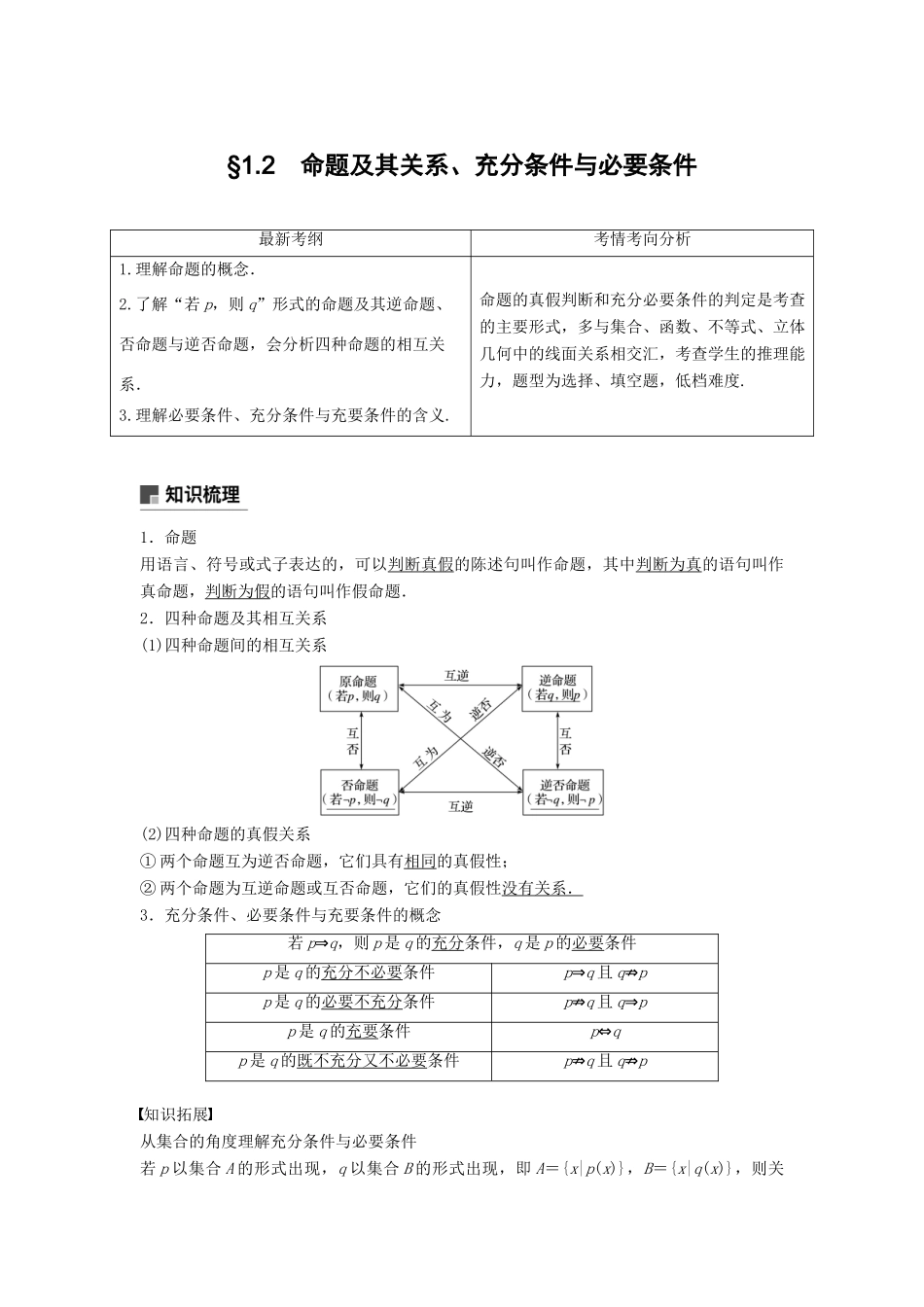
§1.2 命题及其关系、充分条件与必要条件最新考纲考情考向分析1.理解命题的概念.2.了解“若 p,则 q”形式的命题及其逆命题、否命题与逆否命题,会分析四种命题的相互关系.3.理解必要条件、充分条件与充要条件的含义.命题的真假判断和充分必要条件的判定是考查的主要形式,多与集合、函数、不等式、立体几何中的线面关系相交汇,考查学生的推理能力,题型为选择、填空题,低档难度.1.命题用语言、符号或式子表达的,可以判断真假的陈述句叫作命题,其中判断为真的语句叫作真命题,判断为假的语句叫作假命题.2.四种命题及其相互关系(1)四种命题间的相互关系(2)四种命题的真假关系① 两个命题互为逆否命题,它们具有相同的真假性;② 两个命题为互逆命题或互否命题,它们的真假性没有关系.3.充分条件、必要条件与充要条件的概念若 p⇒q,则 p 是 q 的充分条件,q 是 p 的必要条件p 是 q 的充分不必要条件p⇒q 且 q⇏pp 是 q 的必要不充分条件p⇏q 且 q⇒pp 是 q 的充要条件p⇔qp 是 q 的既不充分又不必要条件p⇏q 且 q⇏p知识拓展从集合的角度理解充分条件与必要条件若 p 以集合 A 的形式出现,q 以集合 B 的形式出现,即 A={x|p(x)},B={x|q(x)},则关于充分条件、必要条件又可以叙述为:(1)若 A⊆B,则 p 是 q 的充分条件;(2)若 A⊇B,则 p 是 q 的必要条件;(3)若 A=B,则 p 是 q 的充要条件;(4)若 AB,则 p 是 q 的充分不必要条件;(5)若 AB,则 p 是 q 的必要不充分条件;(6)若 A⃘B 且 A⊉B,则 p 是 q 的既不充分又不必要条件.题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)“对顶角相等”是命题.( √ )(2)命题“若 p,则 q”的否命题是“若 p,则綈 q”.( × )(3)当 q 是 p 的必要条件时,p 是 q 的充分条件.( √ )(4)当 p 是 q 的充要条件时,也可说成 q 成立当且仅当 p 成立.( √ )(5)若 p 是 q 的充分不必要条件,则綈 p 是綈 q 的必要不充分条件.( √ )题组二 教材改编2.下列命题是真命题的是( )A.矩形的对角线相等B.若 a>b,c>d,则 ac>bdC.若整数 a 是素数,则 a 是奇数D.命题“若 x2>0,则 x>1”的逆否命题答案 A3.“x-3=0”是“(x-3)(x-4)=0”的________条件.(填“充分不必要”“必要不充分”“充要”“既不充分又不必要”)答案 充分...