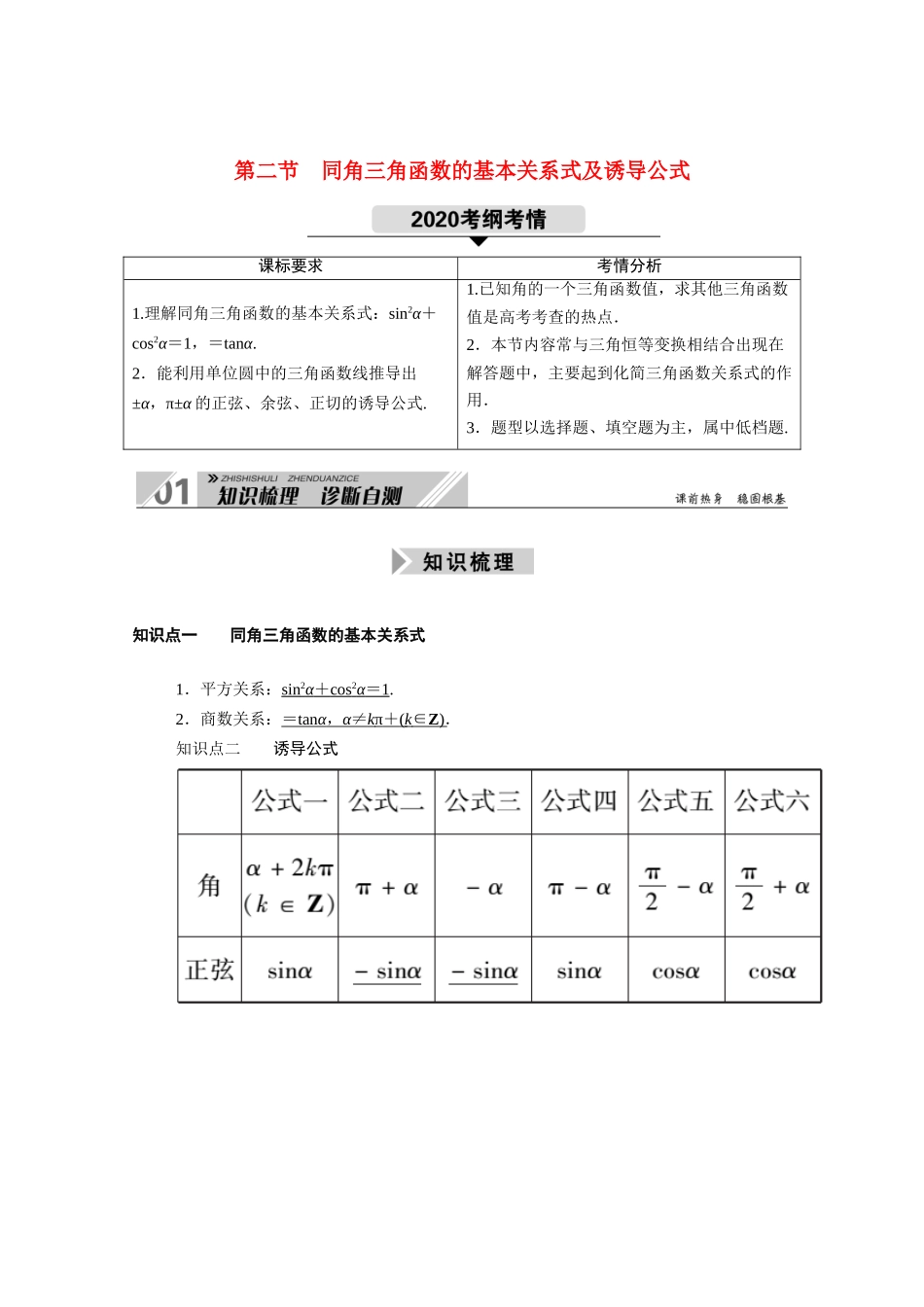
第二节 同角三角函数的基本关系式及诱导公式课标要求考情分析1.理解同角三角函数的基本关系式:sin2α+cos2α=1,=tanα.2.能利用单位圆中的三角函数线推导出±α,π±α 的正弦、余弦、正切的诱导公式.1.已知角的一个三角函数值,求其他三角函数值是高考考查的热点.2.本节内容常与三角恒等变换相结合出现在解答题中,主要起到化简三角函数关系式的作用.3.题型以选择题、填空题为主,属中低档题. 知识点一 同角三角函数的基本关系式1.平方关系:sin 2 α + cos 2 α = 1 .2.商数关系:= tan α , α ≠ k π + ( k ∈ Z ) .知识点二 诱导公式注意以下结论:(1)同角三角函数关系式的常用变形(sinα±cosα)2=1±2sinαcosα;sinα=tanα·cosα.(2)诱导公式的记忆口诀“奇变偶不变,符号看象限”,其中的奇、偶是指的奇数倍和偶数倍,变与不变指函数名称的变化.(3)给角求值的基本原则负化正,大化小,化到锐角为终了.1.思考辨析判断下列结论正误(在括号内打“√”或“×”)(1)若 α,β 为锐角,则 sin2α+cos2β=1.( × )(2)若 α∈R,则 tanα=恒成立.( × )(3)sin(π+α)=-sinα 成立的条件是 α 为锐角.( × )(4)若 sin(kπ-α)=(k∈Z),则 sinα=.( × )解析:(1)根据同角三角函数的基本关系式知当 α,β 为同角时才正确.(2)当 cosα≠0 时才成立.(3)根据诱导公式知 α 为任意角.(4)当 k 为奇数和偶数时,sinα 的值不同.2.小题热身(1)sin210°cos120°的值为( A )A. B.-C.- D.(2)已知 sin=,那么 cosα=( C )A.- B.-C. D.(3)已知 sinα=,α∈,则 tanα=( D )A.-2 B.2C. D.-(4)已知 tanα=2,则的值为 3.(5)若 sinθcosθ=,则 tanθ+=2.解析:(1)sin210°cos120°=-sin30°(-cos60°)=-×=.(2) sin=sin=cosα,∴cosα=.(3)因为≤α≤π,所以 cosα=-=-=-,所以 tanα==-.(4)===3.(5)tanθ+=+==2. 考点一 同角三角函数基本关系的应用命题方向 1 公式直接应用【例 1】 (1)已知 cosα=k,k∈R,α∈,则 sinα=( )A.- B.C.± D.(2)若=3,则 cosα-2sinα=( )A.-1 B.1C.- D.-1 或-【解析】 (1) cos2α+sin2α=1,且 α∈(,π),∴sinα>0,sinα==.(2)由已知得 3sinα=1+cosα>0,cosα=3sinα-1,cos2α=1-sin2α...