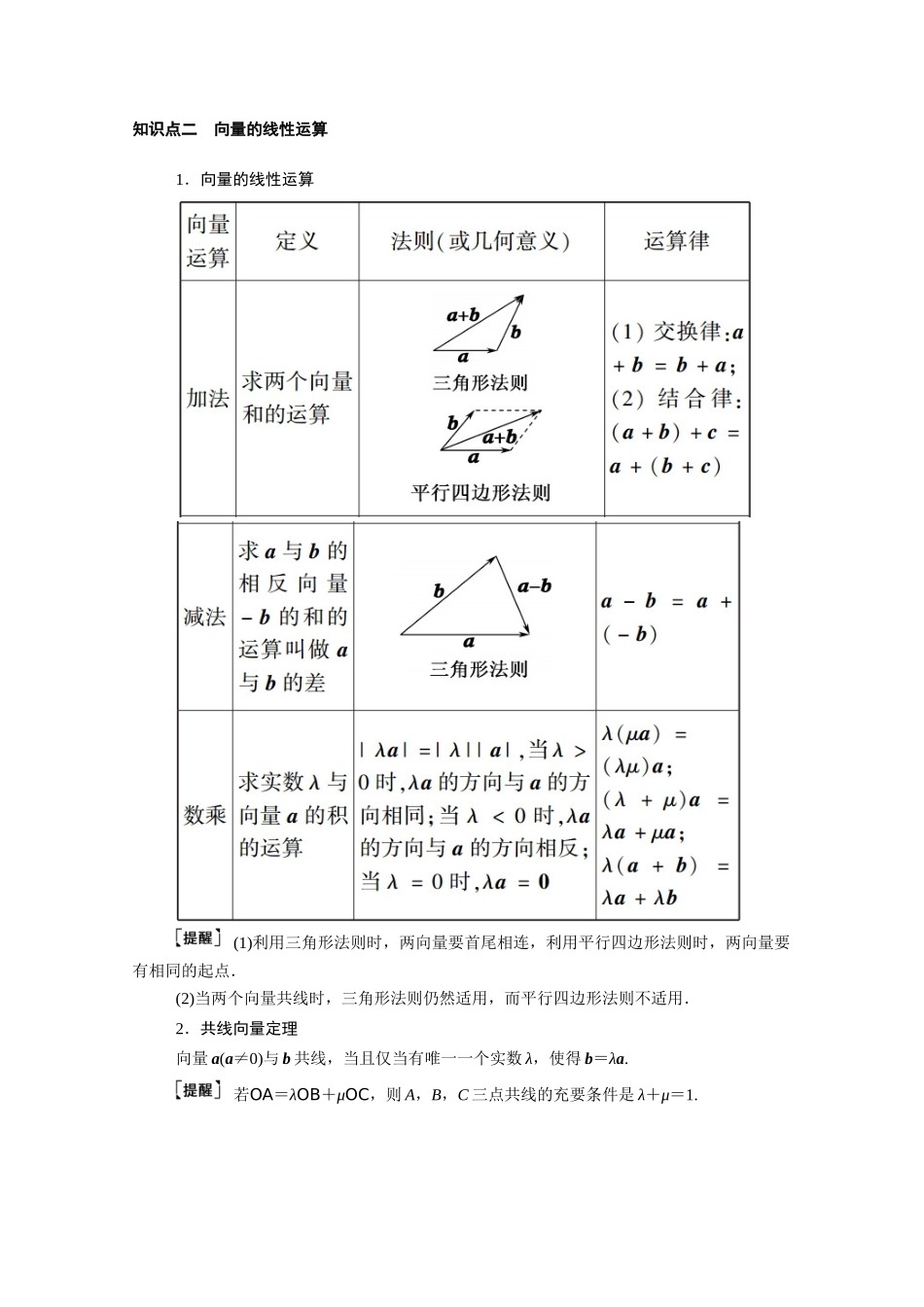
第四章 平面向量、数系的扩充与复数的引入第一节 平面向量的概念及其线性运算课标要求考情分析1
了解向量的实际背景．2．理解平面向量的概念，理解两个向量相等的含义．3．理解向量的几何表示．4．掌握向量加法、减法的运算，并理解其几何意义．5．掌握向量数乘的运算及其几何意义，理解两个向量共线的含义．6．了解向量线性运算的性质及其几何意义．1
平面向量的线性运算、共线向量定理是近几年高考命题的热点．2．常与三角、平面几何知识交汇考查，有时也会命制新定义问题．3．题型以选择题、填空题为主，属中低档题
知识点一 向量的有关概念名称定义备注向量既有大小又有方向的量；向量的大小叫做向量的长度(或称模)平面向量是自由向量零向量长度为 0 的向量记作 0，其方向是任意的单位向量长度等于 1 个单位的向量非零向量 a 的单位向量为±平行向量方向相同或相反的非零向量(又叫做共线向量)0 与任一向量平行或共线相等向量长度相等且方向相同的向量两向量只有相等或不相等，不能比较大小相反向量长度相等且方向相反的向量0 的相反向量为 0向量概念的四点注意(1)注意 0 与 0 的区别，0 是一个实数，0 是一个向量，且|0|＝0
(2)单位向量有无数个，它们的模相等，但方向不一定相同．(3)零向量和单位向量是两个特殊的向量，它们的模是确定的，但是方向不确定，因此在解题时要注意它们的特殊性．(4)任一组平行向量都可以平移到同一直线上．知识点二 向量的线性运算1．向量的线性运算(1)利用三角形法则时，两向量要首尾相连，利用平行四边形法则时，两向量要有相同的起点．(2)当两个向量共线时，三角形法则仍然适用，而平行四边形法则不适用．2．共线向量定理向量 a(a≠0)与 b 共线，当且仅当有唯一一个实数 λ，使得 b＝λa
若OA＝λOB＋μOC，则 A，B，C 三点共线的充要条件是 λ＋μ＝1
1．思考辨析判断下列
