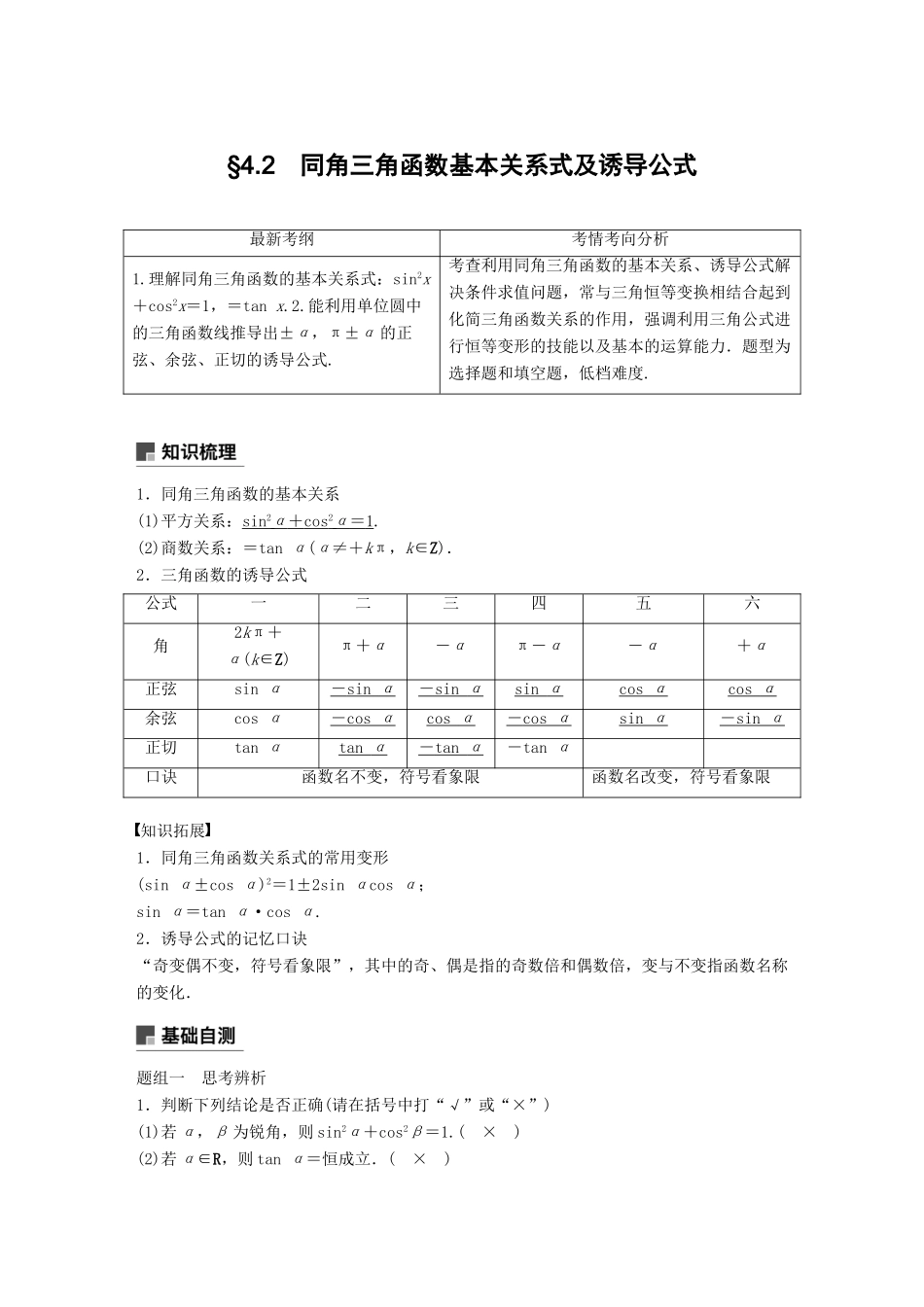
§4.2 同角三角函数基本关系式及诱导公式最新考纲考情考向分析1.理解同角三角函数的基本关系式:sin2x+cos2x=1,=tan x.2.能利用单位圆中的三角函数线推导出±α,π±α 的正弦、余弦、正切的诱导公式.考查利用同角三角函数的基本关系、诱导公式解决条件求值问题,常与三角恒等变换相结合起到化简三角函数关系的作用,强调利用三角公式进行恒等变形的技能以及基本的运算能力.题型为选择题和填空题,低档难度.1.同角三角函数的基本关系(1)平方关系:sin 2 α + cos 2 α = 1 .(2)商数关系:=tan α(α≠+kπ,k∈Z).2.三角函数的诱导公式公式一二三四五六角2kπ+α(k∈Z)π+α-απ-α-α+α正弦sin α- sin α - sin α sin α cos α cos α 余弦cos α- cos α cos α - cos α sin α - sin α 正切tan αtan α - tan α -tan α口诀函数名不变,符号看象限函数名改变,符号看象限知识拓展1.同角三角函数关系式的常用变形(sin α±cos α)2=1±2sin αcos α;sin α=tan α·cos α.2.诱导公式的记忆口诀“奇变偶不变,符号看象限”,其中的奇、偶是指的奇数倍和偶数倍,变与不变指函数名称的变化.题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)若 α,β 为锐角,则 sin2α+cos2β=1.( × )(2)若 α∈R,则 tan α=恒成立.( × )(3)sin(π+α)=-sin α 成立的条件是 α 为锐角.( × )(4)若 sin(kπ-α)=(k∈Z),则 sin α=.( × )题组二 教材改编2.[P19 例 6]若 sin α=,<α<π,则 tan α= .答案 -解析 <α<π,∴cos α=-=-,∴tan α==-.3.[P22B 组 T3]已知 tan α=2,则的值为 .答案 3解析 原式===3.4.[P28T7]化简·sin(α-π)·cos(2π-α)的结果为 .答案 -sin2α解析 原式=·(-sin α)·cos α=-sin2α.题组三 易错自纠5.(2017·贵阳模拟)已知 sin αcos α=,且<α<,则 cos α-sin α 的值为( )A.- B.C.- D.答案 B解析 <α<,∴cos α<0,sin α<0 且 cos α>sin α,∴cos α-sin α>0.又(cos α-sin α)2=1-2sin αcos α=1-2×=,∴cos α-sin α=.6.已知 sin(π-α)=log8,且 α∈,则 tan(2π-α)的值为( )A.- B.C.± D.答案 B解析 sin(π-α)=si...