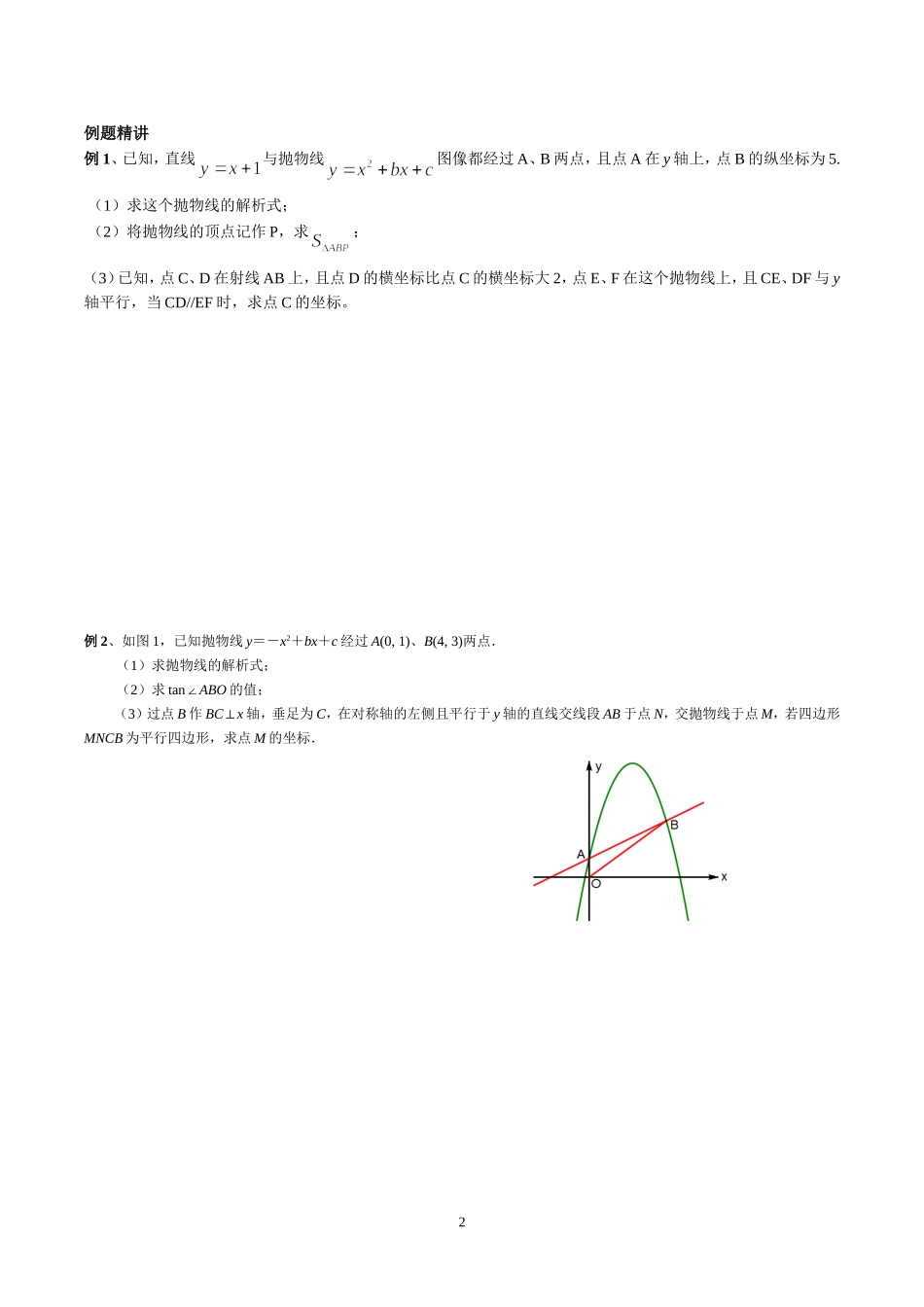
1中考数学专题练习————————因动点产生特殊四边形 中考数学的动点题型中,因动点产生特殊四边形的问题的讨论一般包括平行四边形和梯形的讨论。 解平行四边形的存在性问题一般分为三个步骤:(1)寻找分类目标;(2)画出适当的图形;(3)利用相关数据进行计算。难点在于寻找分类标准,寻找恰当的分类标准,可以使得解的个数不重复、不遗漏,也可以使得计算又准又快。如果已知三个定点,探寻平行四边形的第四个顶点,符合条件的有三个点:以已知三个定点为三角形的顶点,过每个点画对边的平行线,三条平行线两两相交,产生 3 个当。如果已知两个定点,一般是把确定的一条线段按照边或对角线分为两种情况。灵活应用向量和中心对称的性质,可以使得解题更简便。解梯形存在性问题,一般是已知三角形的三个顶点,在某个图像上求第四个顶点,使得四个顶点围成梯形。过三角形的每个顶点画对边的平行线,这条直线与图像的交点就是要探寻的梯形的顶点。灵活应用相似比列方程,可以使得解题简便。热身练习1、如图,梯形 ABCD 中,AD=12,BC=16,动点 P 在边 CB 上从 C 往 B 运动,速度是每秒 1 个单位;动点 Q 在边 AD 上从 A 往 D 运动,速度也是每秒 1 个单位,动点 P、Q 只要其中一个到达终点,另一点也随之停止运动。设:运动时间为 t。 (1)t 为何值时,四边形 ABPQ 为平行四边形? (2)t 为何值时,四边形 CDQP 为矩形? (3)t 为何值时,AB=PQ?2、抛物线经过直线与坐标轴的两个交点 A、B,此抛物线与 x 轴的另一交点为 C、顶点为 D。 (1)求此抛物线的解析式; (2)点 P 为抛物线上的一动点,求使时点 P 的坐标; (3)点 M 为平面直角坐标系上的一点,写出使点 M、A、B、D 为平行四边形的点 M 的坐标。QPDABC2例题精讲例 1、已知,直线与抛物线图像都经过 A、B 两点,且点 A 在 y 轴上,点 B 的纵坐标为 5. (1)求这个抛物线的解析式; (2)将抛物线的顶点记作 P,求; (3)已知,点 C、D 在射线 AB 上,且点 D 的横坐标比点 C 的横坐标大 2,点 E、F 在这个抛物线上,且 CE、DF 与 y轴平行,当 CD//EF 时,求点 C 的坐标。例 2、如图 1,已知抛物线 y=-x2+bx+c 经过 A(0, 1)、B(4, 3)两点. (1)求抛物线的解析式;(2)求 tan∠ABO 的值;(3)过点 B 作 BC⊥x 轴,垂足为 C,在对称轴的左侧且平行于 y 轴的直...