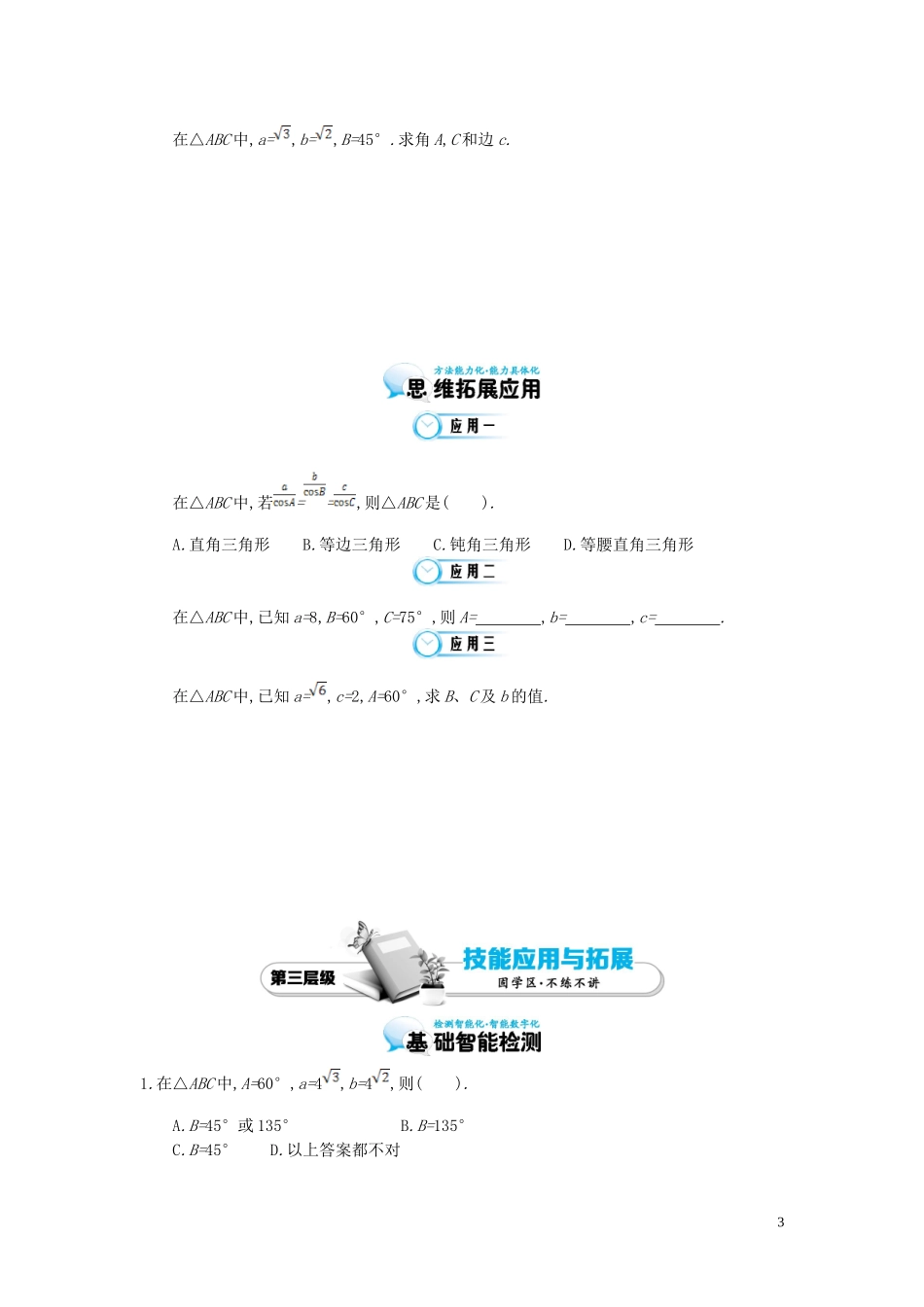
第 1 课时 正 弦 定 理1.掌握正弦定理及其证明过程.2.根据已知三角形的边和角,利用正弦定理解三角形.3.能根据正弦定理及三角变换公式判断三角形的形状.古埃及时代,尼罗河经常泛滥,古埃及人为了研究尼罗河水运行的规律,准备测量各种数据.当尼罗河涨水时,古埃及人想测量某处河面的宽度(如图),如果古埃及人通过测量得到了AB 的长度,∠BAC,∠ABC 的大小,那么就可以求解出河面的宽度 CD,古埃及人是如何利用这些数据计算的呢?问题 1:在上面的问题中, △ABC 的已知元素有 和边 . 若 AB=2,∠ABC=30°,∠BAC=120°,则 BC= ,CD= . 解三角形: 的过程. 问题 2:正弦定理:在一个三角形中,各边和它所对的角的正弦的比相等,即 . 问题 3:正弦定理的拓展:①a∶b∶c= ; ② 设 R 为△ABC 外接圆的半径,则=== . 问题 4:在△ABC 中,已知 a、b 和 A 时,解的情况如下:A 为锐角A 为钝角或直角图形关系式 ① ② ③ 解的个数一解两解一解一解11.在△ABC 中,下列等式总能成立的是( ).A.acos C=ccos A B.bsin C=csin AC.absin C=bcsin B D.asin C=csin A2.已知△ABC 中,a=4,b=5,A=30°.下列对三角形解的情况的判断中,正确的是( ).A.一解B.两解C.无解D.一解或无解3.在△ABC 中,已知 a=5,c=10,A=30°,则 B 等于 . 4.在△ABC 中,已知 b=5,B= ,tan A=2,求 sin A 和边 a.利用正弦定理判断三角形的形状在△ABC 中,若 sin A=2sin Bcos C,且 sin2A=sin2B+sin2C,试判断△ABC 的形状.已知两角及其中一角的对边,解三角形在△ABC 中,已知 c=10,A=45°,C=30°,解这个三角形.已知两边及其中一边的对角,解三角形2在△ABC 中,a=,b=,B=45°.求角 A,C 和边 c.在△ABC 中,若==,则△ABC 是( ).A.直角三角形 B.等边三角形C.钝角三角形 D.等腰直角三角形在△ABC 中,已知 a=8,B=60°,C=75°,则 A= ,b= ,c= . 在△ABC 中,已知 a=,c=2,A=60°,求 B、C 及 b 的值.1.在△ABC 中,A=60°,a=4,b=4,则( ).A.B=45°或 135° B.B=135°C.B=45°D.以上答案都不对32.△ABC 的内角 A,B,C 的对边分别为 a,b,c,若 c=,b=,B=120°,则 a 等于( ).A. B.2 C. D.3.在△ABC 中,cos A= ,cos B= ,则△ABC 中三边的比值 a∶b∶c= . 4.在△ABC 中,若 B=60°,AC=3,AB=,求 A.(2013 年·北京卷)在△ABC 中,a=3,b=5,sin A= ,则 sin B 等于( ).A.B.C.D.1考题变式(我来改编):4第二章 解...