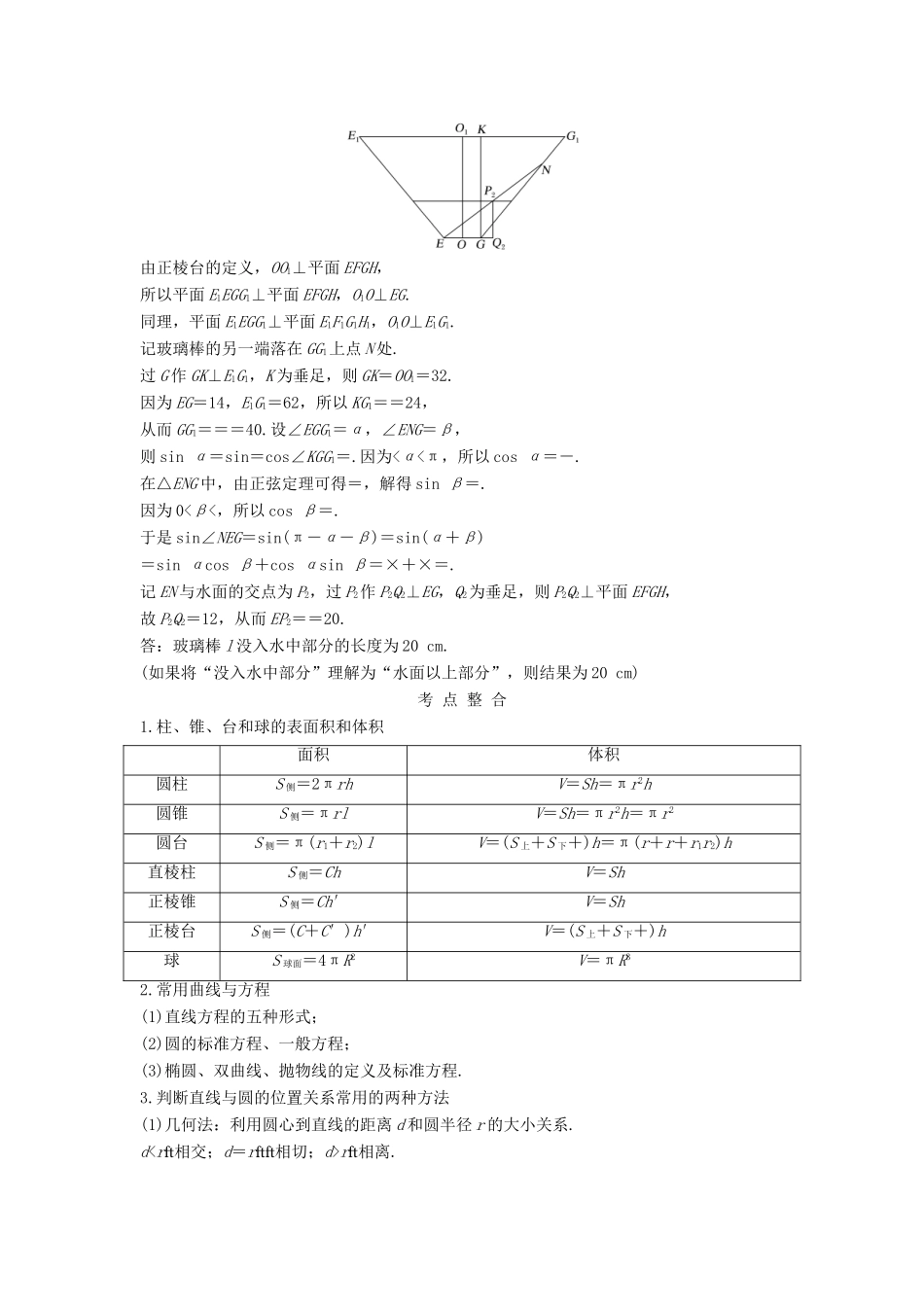
第 3 讲 立体几何与解析几何应用题高考定位 高考对本内容的考查主要有:(1)以空间几何体及其表面积和体积为载体的立体几何应用题;(2)以坐标系、曲线与方程为载体的解析几何应用题.真 题 感 悟 (2017·江苏卷)如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为 32 cm,容器Ⅰ的底面对角线 AC 的长为 10 cm,容器Ⅱ的两底面对角线 EG,E1G1的长分别为 14 cm 和 62 cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为 12 cm.现有一根玻璃棒l,其长度为 40 cm.(容器厚度、玻璃棒粗细均忽略不计).(1)将 l 放在容器Ⅰ中,l 的一端置于点 A 处,另一端置于侧棱 CC1上,求 l 没入水中部分的长度;(2)将 l 放在容器Ⅱ中,l 的一端置于点 E 处,另一端置于侧棱 GG1上,求 l 没入水中部分的长度.解 (1)由正棱柱的定义,CC1⊥平面 ABCD,所以平面 A1ACC1⊥平面 ABCD,CC1⊥AC.记玻璃棒的另一端落在 CC1上点 M 处.因为 AC=10,AM=40,所以 MC==30,从而 sin∠MAC=.记 AM 与水面的交点为 P1,过 P1作 P1Q1⊥AC,Q1为垂足,则 P1Q1⊥平面 ABCD,故 P1Q1=12,从而 AP1==16.答:玻璃棒 l 没入水中的部分的长度为 16 cm.(如果将“没入水中部分”理解为“水面以上部分”,则结果为 24 cm)(2)如图,O,O1是正棱台的两底面中心.由正棱台的定义,OO1⊥平面 EFGH,所以平面 E1EGG1⊥平面 EFGH,O1O⊥EG.同理,平面 E1EGG1⊥平面 E1F1G1H1,O1O⊥E1G1.记玻璃棒的另一端落在 GG1上点 N 处.过 G 作 GK⊥E1G1,K 为垂足,则 GK=OO1=32.因为 EG=14,E1G1=62,所以 KG1==24,从而 GG1===40.设∠EGG1=α,∠ENG=β,则 sin α=sin=cos∠KGG1=.因为<α<π,所以 cos α=-.在△ENG 中,由正弦定理可得=,解得 sin β=.因为 0<β<,所以 cos β=.于是 sin∠NEG=sin(π-α-β)=sin(α+β)=sin αcos β+cos αsin β=×+×=.记 EN 与水面的交点为 P2,过 P2作 P2Q2⊥EG,Q2为垂足,则 P2Q2⊥平面 EFGH,故 P2Q2=12,从而 EP2==20.答:玻璃棒 l 没入水中部分的长度为 20 cm.(如果将“没入水中部分”理解为“水面以上部分”,则结果为 20 cm)考 点 整 合1.柱、锥、台和球的表面积和体积面积体积圆柱S 侧=2πrhV=Sh=πr2h圆锥S 侧=πrlV=Sh=πr2h=πr2圆台S 侧=π(r1+r2)lV=(S 上+S 下+)h=...