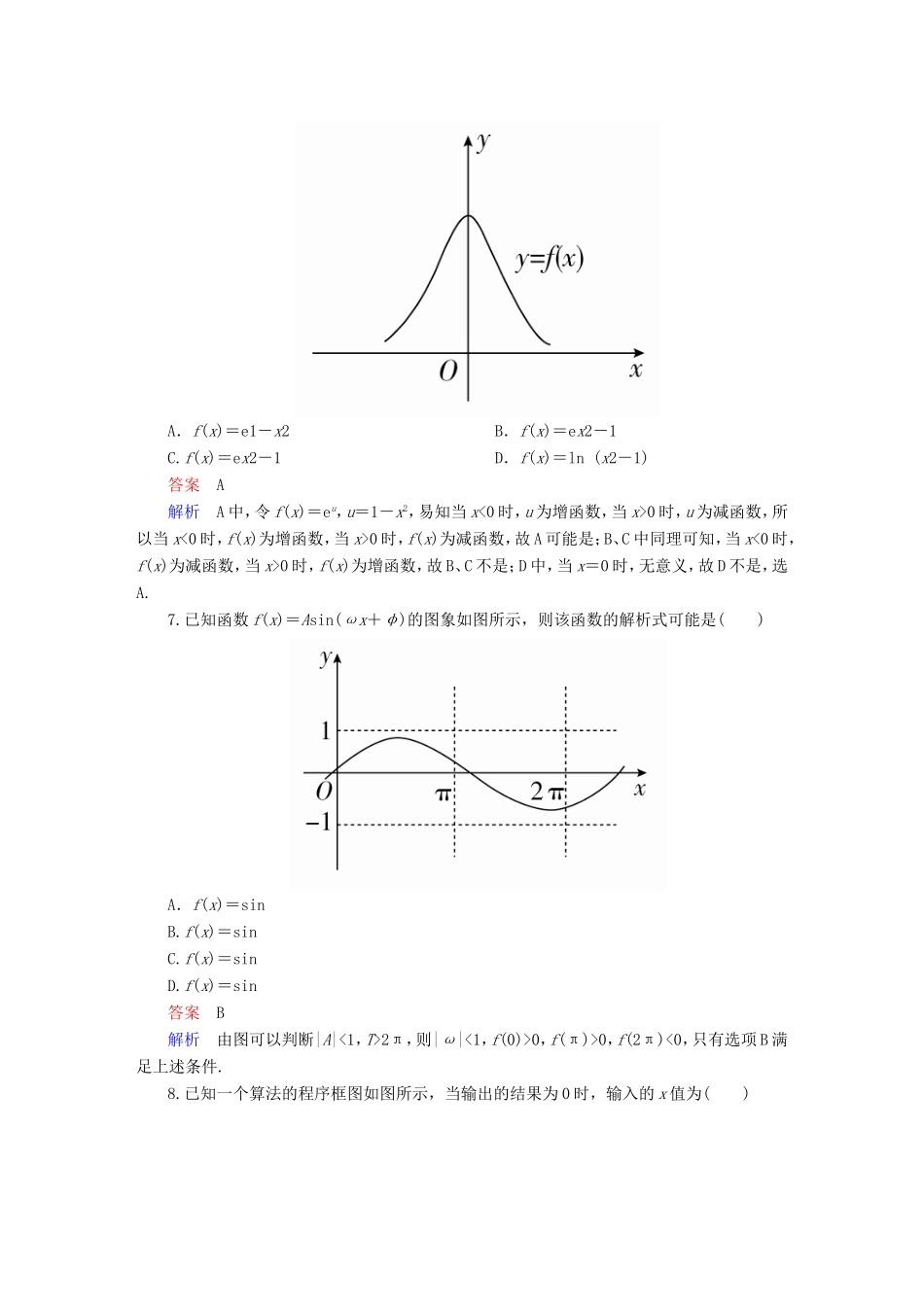
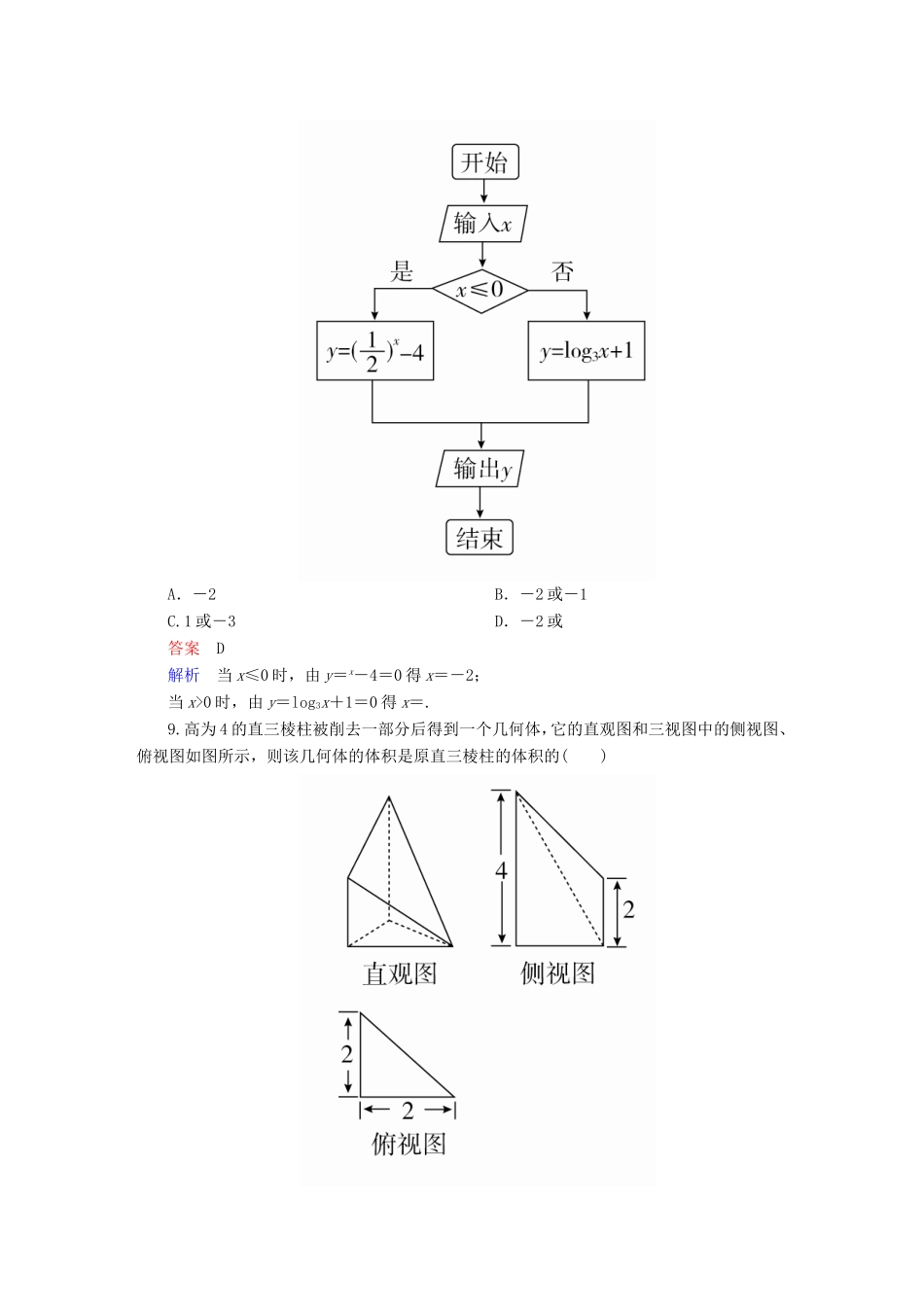
第三步应试技能专训一、客观题专练(一)一、选择题1.设U=R,集合A=,B={x∈R|00),故选C.4.(x2-2)5的展开式中x-1的系数为()A.60B.50C.40D.20答案A解析由通项公式得展开式中x-1的系数为23C-22C=60.5.已知变量x,y满足约束条件则z=2x+y的最大值为()A.1B.2C.3D.4答案B解析画出可行域得知,当直线y=z-2x过点(1,0)时,z取得最大值2.6.已知函数f(x)的图象如图所示,则f(x)的解析式可能是()A.f(x)=e1-x2B.f(x)=ex2-1C.f(x)=ex2-1D.f(x)=ln(x2-1)答案A解析A中,令f(x)=eu,u=1-x2,易知当x<0时,u为增函数,当x>0时,u为减函数,所以当x<0时,f(x)为增函数,当x>0时,f(x)为减函数,故A可能是;B、C中同理可知,当x<0时,f(x)为减函数,当x>0时,f(x)为增函数,故B、C不是;D中,当x=0时,无意义,故D不是,选A.7.已知函数f(x)=Asin(ωx+φ)的图象如图所示,则该函数的解析式可能是()A.f(x)=sinB.f(x)=sinC.f(x)=sinD.f(x)=sin答案B解析由图可以判断|A|<1,T>2π,则|ω|<1,f(0)>0,f(π)>0,f(2π)<0,只有选项B满足上述条件.8.已知一个算法的程序框图如图所示,当输出的结果为0时,输入的x值为()A.-2B.-2或-1C.1或-3D.-2或答案D解析当x≤0时,由y=x-4=0得x=-2;当x>0时,由y=log3x+1=0得x=.9.高为4的直三棱柱被削去一部分后得到一个几何体,它的直观图和三视图中的侧视图、俯视图如图所示,则该几何体的体积是原直三棱柱的体积的()A.B.C.D.答案C解析由侧视图、俯视图知该几何体是高为2、底面积为×2×(2+4)=6的四棱锥,其体积为4.易知直三棱柱的体积为8,则该几何体的体积是原直三棱柱的体积的=,故选C.10.[2016·贵阳监测]已知双曲线-=1(a>0,b>0)与函数y=的图象交于点P,若函数y=的图象在点P处的切线过双曲线左焦点F(-2,0),则双曲线的离心率是()A.B.C.D.答案B解析设P(x0,),因为函数y=的导数为y′=,所以切线的斜率为.又切线过双曲线的左焦点F(-2,0),所以=,解得x0=2,所以P(2,).因为点P在双曲线上,所以-=1①.又c2=22=a2+b2②,联立①②解得a=或a=2(舍),所以e===,故选B.11.[2015·山西四校联考]在正三棱锥S-ABC中,M是SC的中点,且AM⊥SB,底面边长AB=2,则正三棱锥S-ABC的外接球的表面积为()A.6πB.12πC.32πD.36π答案B解析如图,取CB的中点N,连接MN,AN,则MN∥SB.由于AM⊥SB,所以AM⊥MN.由正三棱锥的性质易知SB⊥AC,结合AM⊥SB知SB⊥平面SAC,所以SB⊥SA,SB⊥SC.又正三棱锥的三个侧面是全等的三角形,所以SA⊥SC,所以正三棱锥S-ABC为正方体的一个角,所以正三棱锥S-ABC的外接球即为正方体的外接球.由AB=2,得SA=SB=SC=2,所以正方体的体对角线为2,所以所求外接球的半径R=,其表面积为4πR2=12π,故选B.12.[2016·重庆质检]设f′(x)是函数f(x)的导函数,且f′(x)>2f(x)(x∈R),f=e(e为自然对数的底数),则不等式f(lnx)0,因此函数g(x)在R上是增函数,且g==1.不等式f(lnx)