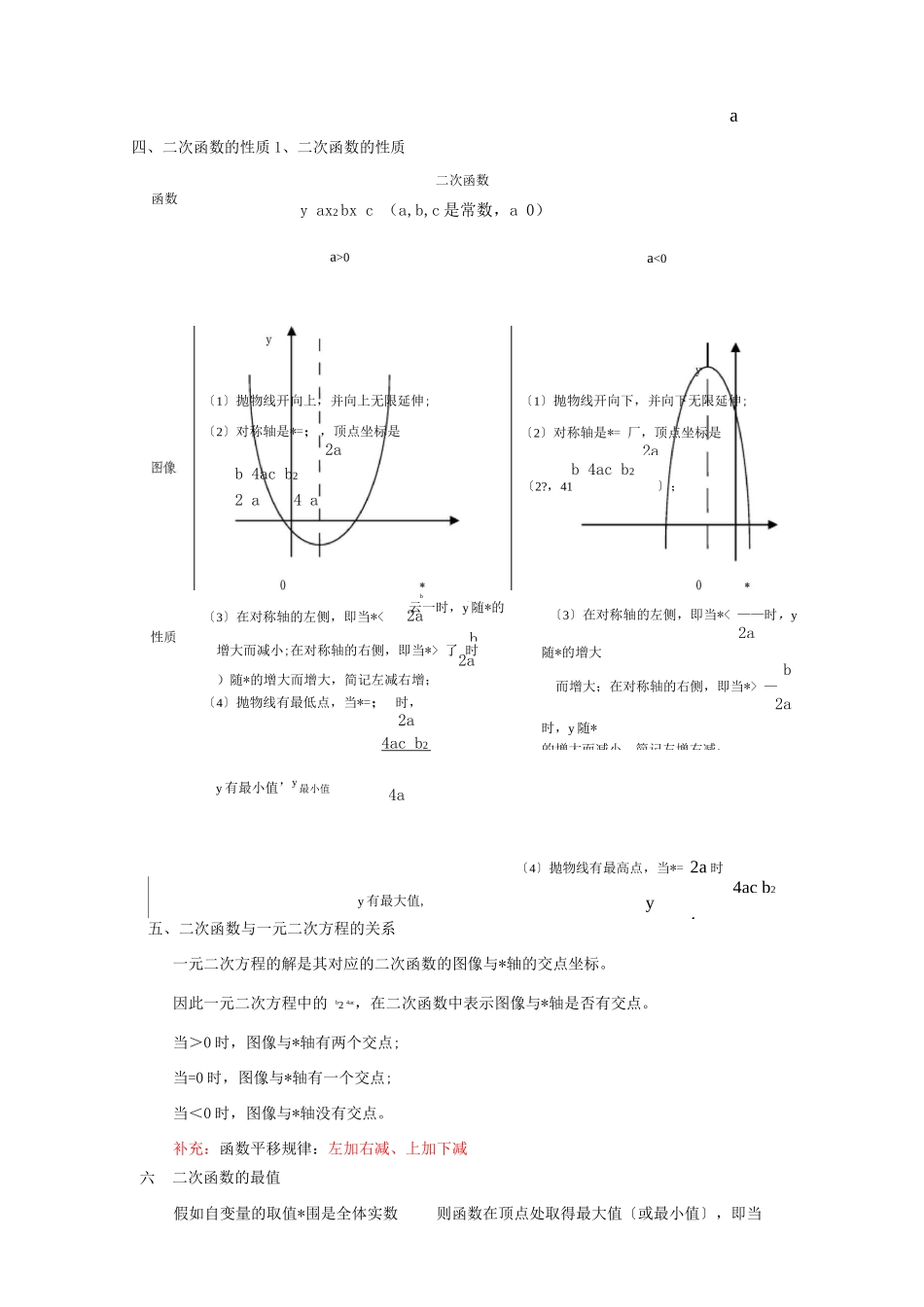
二次函数知识点总结及典型例题一、二次函数的概念和图像1、二次函数的概念一般地,假如 y ax2 bx c(a,b,c 是常数,a 。),则 y 叫做*的二次函数。y ax2bx c(a,b,c 是常数,a 0)叫做二次函数的一般式。2、二次函数的图像二次函数的图像是一条关于 x&对称的曲线,这条曲线叫抛物线。抛物线的主要特征:① 有开方向;②有对称轴;③有顶点。3、二次函数图像的画法---五点法:二、二次函数的解析式二次函数的解析式有三种形式:〔1〕一般式:yax2 bxc (a,b,c 是常数,a 0)〔2〕顶点式:ya (x h)2k(a,h,k 是常数,a 0)〔3〕当抛物线 yax2 bxc与*轴有交点时,即对应二次好方程 ax2 bx c 0有实根 x 和 x 存在时,根据二次三项式的分解因式 ax2 bx c a (x x ) x x ),二次 1212函数 y ax2 bxC 可转化为两根式 y a(x x「x x「。假如没有交点,则不能这样表示。三、抛物线 y ax2 bx c 中,a,b,c 的作用〔1〕a 决定开方向及开大小,这与 y ax2中的 a 完全一样.〔2〕b 和 a 共同决定抛物线对称轴的位置.由于抛物线 y ax2 bx c 的对称轴是直线x ?,故:① b 0 时,对称轴为 y 轴所在直线;②^ 0〔即 a、b同号〕时,2aa对称轴在 y 轴左侧;③^ 0〔即 a、b 异号〕时,对称轴在 y 轴右侧.a〔3〕c 的大小决定抛物线 y ax2 bx c 与 y 轴交点的位置.当 x 0 时,y c,.・.抛物线 y ax2 bx c 与 y 轴有且只有一个交点〔0, c〕:①c 0,抛物线经过原点;② c 0,与 y 轴交于正半轴;③ c 0,与 y 轴交于负半轴.以上三点中,当结论和条件互换时,仍成立.如抛物线的对称轴在 y 轴右侧,则 b0.a四、二次函数的性质 1、二次函数的性质二次函数y ax2 bx c (a,b,c 是常数,a 0)a>0〔4〕抛物线有最高点,当*= 2a 时4ac b2y 有最大值,y最大值4a五、二次函数与一元二次方程的关系一元二次方程的解是其对应的二次函数的图像与*轴的交点坐标。因此一元二次方程中的 b2 4ac,在二次函数中表示图像与*轴是否有交点。当>0 时,图像与*轴有两个交点;当=0 时,图像与*轴有一个交点;当<0 时,图像与*轴没有交点。补充:函数平移规律:左加右减、上加下减函数a<0〔1〕抛物线开向上,并向上无限延伸;〔2〕对称轴是*=;,顶点坐标是2ab 4ac b22 a4 a〔1〕抛物线开向下,并向下无限延伸;〔2〕对称轴是*= 厂,顶点坐标是2ab 4ac b2〔2?,41...