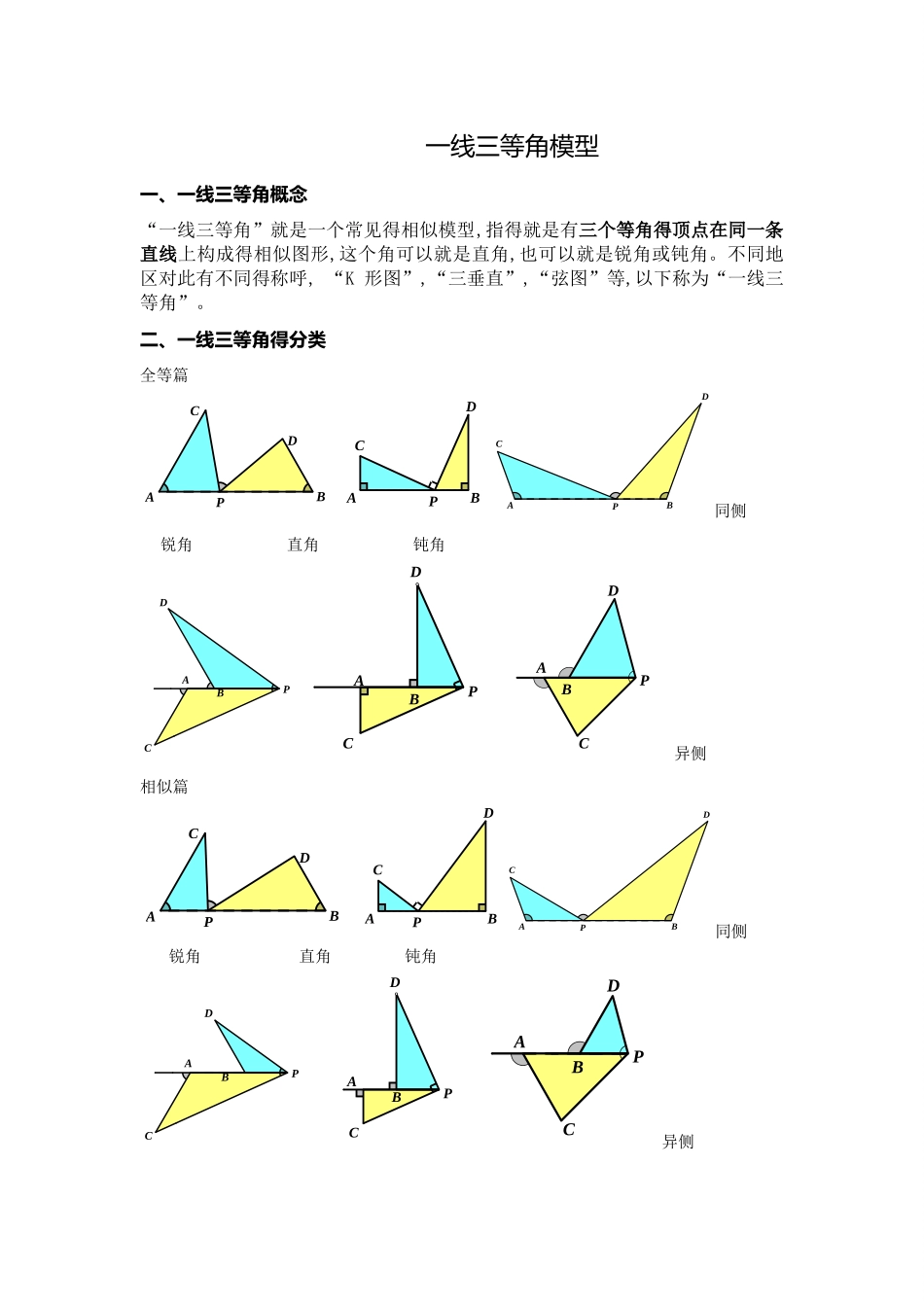
一线三等角模型一、一线三等角概念“一线三等角”就是一个常见得相似模型,指得就是有三个等角得顶点在同一条直线上构成得相似图形,这个角可以就是直角,也可以就是锐角或钝角。不同地区对此有不同得称呼, “K 形图”,“三垂直”,“弦图”等,以下称为“一线三等角”。二、一线三等角得分类全等篇DCABP DCBAP CABPD同侧 锐角 直角 钝角CDPBA ADPCB DPBCA 异侧相似篇DCABP DCBAPCABPD同侧 锐角 直角 钝角DCPBA CDPBA DPCAB 异侧三、“一线三等角”得性质1、一般情况下,如图 3-1,由∠1=∠2=∠3,易得△AEC∽△BDE、2、当等角所对得边相等时,则两个三角形全等、如图 3-1,若 CE=ED,则△AEC≌△BDE、3、中点型“一线三等角”如图 3-2,当∠1=∠2=∠3,且 D 就是 BC 中点时,△BDE∽△CFD∽△DFE、4、“中点型一线三等角“得变式(了解)如图 3-3,当∠1=∠2 且时,点 O 就是△ABC 得内心、可以考虑构造“一线三等角”、如图 3-4“中点型一线三等角”通常与三角形得内心或旁心相关, 这就是内心得性质,反之未必就是内心、在图 3-4(右图)中,假如延长 BE 与 CF,交于点 P,则点 D 就是△PEF 得旁心、5、“一线三等角”得各种变式(图 3-5,以等腰三角形为例进行说明 )图 3-5其实这个第 4 图,延长 DC 反而好理解、相当于两侧型得,不延长理解,以为就是一种新型得,同侧穿越型?不管怎么变,都就是由三等角确定相似三角形来进行解题四、“一线三等角”得应用1、“一线三等角”应用得三种情况、a、图形中已经存在“一线三等角”,直接应用模型解题;b、图形中存在“一线二等角”,不上“一等角”构造模型解题;c、图形中只有直线上一个角,不上“二等角”构造模型解题、体会:感觉最后一种情况出现比较多,尤其就是压轴题中,常常会有一个特别角或指导该角得三角函数值时,我常常构造“一线三等角”来解题、2、在定边对定角问题中,构造一线三等角就是基本手段,尤其就是直角坐标系中得张角问题,在 x 轴或 y 轴(也可以就是平行于 x 轴或 y 轴得直线)上构造一线三等角解决问题更就是重要得手段、3、构造一线三等角得步骤:找角、定线、构相似坐标系中,要讲究“线”得特别性如图 3-6,线上有一特别角,就考虑构造同侧型一线三等角当然只加这两条线通常就是不够得,为了利用这个特别角导线段得关系,过 C、D 两点作直线 l 得垂线就是必不可少得。两条垂线通常情况下就是为了“量化”得需要。上面就就是作辅助线得一般程序,瞧起来线...