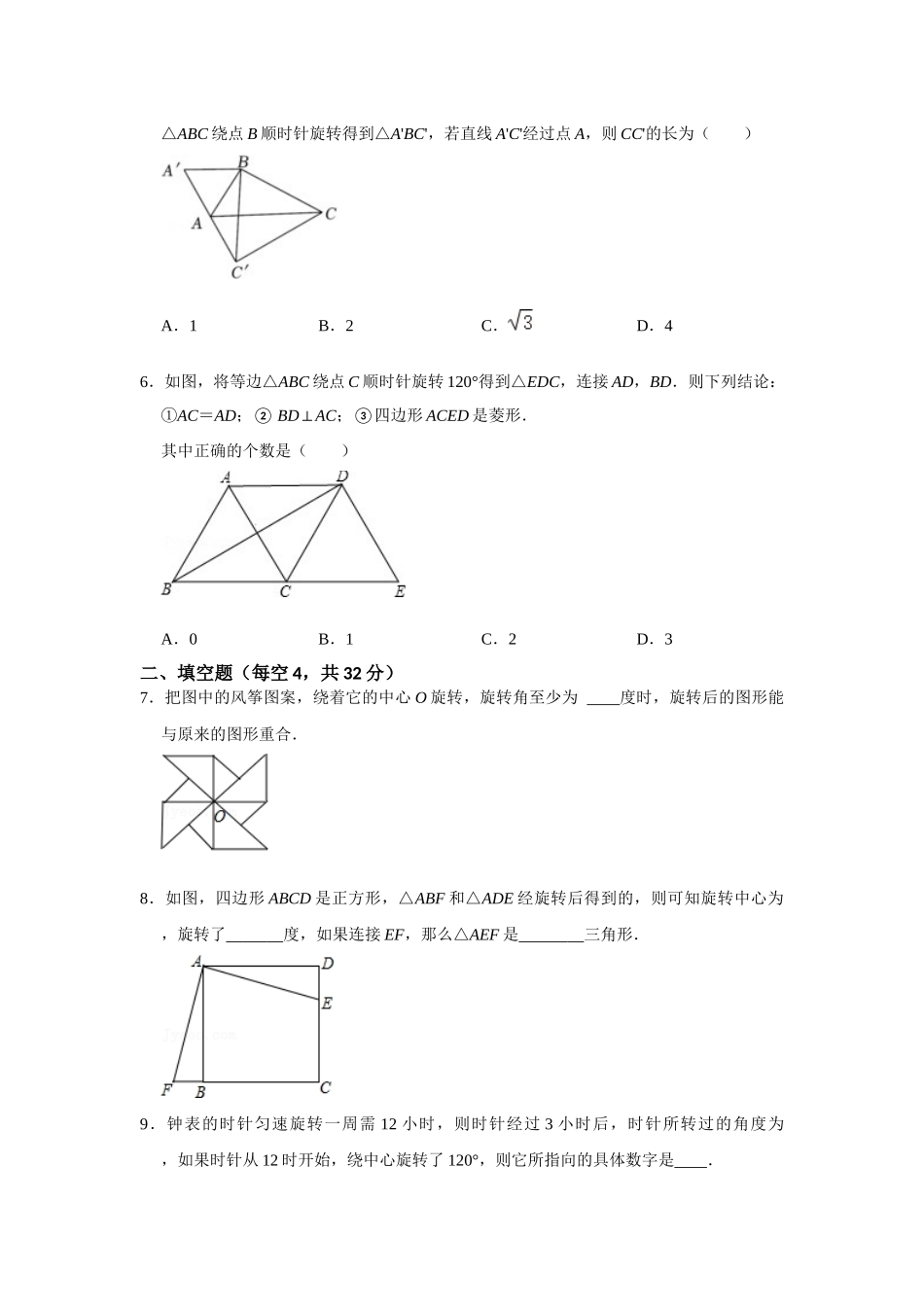
专题 23.1 旋转测试卷一 满分:100 分 时间:45 分钟一、选择题(每小题 4 分,共 24 分)1.下列现象:①时针的转动;②摩天轮的转动;③地下水位逐年下降;④传送带上的机器人.其中,属于旋转的是( )A.①②B.②③C.①④D.③④2.如图所示,△ABC 绕点 A 旋转至△AEF,其旋转角是( )A.∠BAEB.∠CAEC.∠EAFD.∠BAF3.如图,在等边三角形 ABC 中,AB=6,D 是 BC 上一点,且 BC=3BD,△ABD 绕点 A旋转后得到△ACE,则 CE 的长度为( )A.6B.5C.3D.24.(2025•道里区一模)如图,将△ABC 绕点 B 逆时针旋转 80°得△DBE,点 D,E 分别为点 A,C 的对应顶点,连接 AD,若 AD∥BC,则∠DBE 为( )A.80°B.50°C.55°D.100°5.(2024 秋•甘井子区期末)如图,Rt△ABC 中,∠ABC=90°,∠BAC=60°,AB=1,将△ABC 绕点 B 顺时针旋转得到△A'BC',若直线 A'C'经过点 A,则 CC'的长为( )A.1B.2C.D.46.如图,将等边△ABC 绕点 C 顺时针旋转 120°得到△EDC,连接 AD,BD.则下列结论:①AC=AD;② BD⊥AC;③四边形 ACED 是菱形.其中正确的个数是( )A.0B.1C.2D.3二、填空题(每空 4,共 32 分)7.把图中的风筝图案,绕着它的中心 O 旋转,旋转角至少为 度时,旋转后的图形能与原来的图形重合.8.如图,四边形 ABCD 是正方形,△ABF 和△ADE 经旋转后得到的,则可知旋转中心为 ,旋转了 度,如果连接 EF,那么△AEF 是 三角形.9.钟表的时针匀速旋转一周需 12 小时,则时针经过 3 小时后,时针所转过的角度为 ,如果时针从 12 时开始,绕中心旋转了 120°,则它所指向的具体数字是 .10.如图,将△ABC 绕点 C 按顺时针方向旋转至△A'B'C,使点 A'落在 BC 的延长线上.已知∠A=27°,∠B=40°,则∠ACB'= 度.11.如图,已知 Rt△ABC 中,∠ACB=90°,AC=6,BC=4,将△ABC 绕直角顶点 C 顺时针旋转 90°得到△DEC.若点 F 是 DE 的中点,连接 AF,则 AF= .三、解答题(共 44 分)12.(6 分)作图:如图,边长为 1 的小正方形组成的方格纸上,将△ABC 绕着点 A 顺时针旋转 90°.画出旋转后的△AB′C′.13.(12 分)如图,四边形 ABCD 是正方形,△ADF 按顺时针方向旋转一定角度后得到△ABE,点 E 落在 AD 边上,若 AF=4.AB=7.(1)旋转中心为 ;旋转角度为 ;(2)...