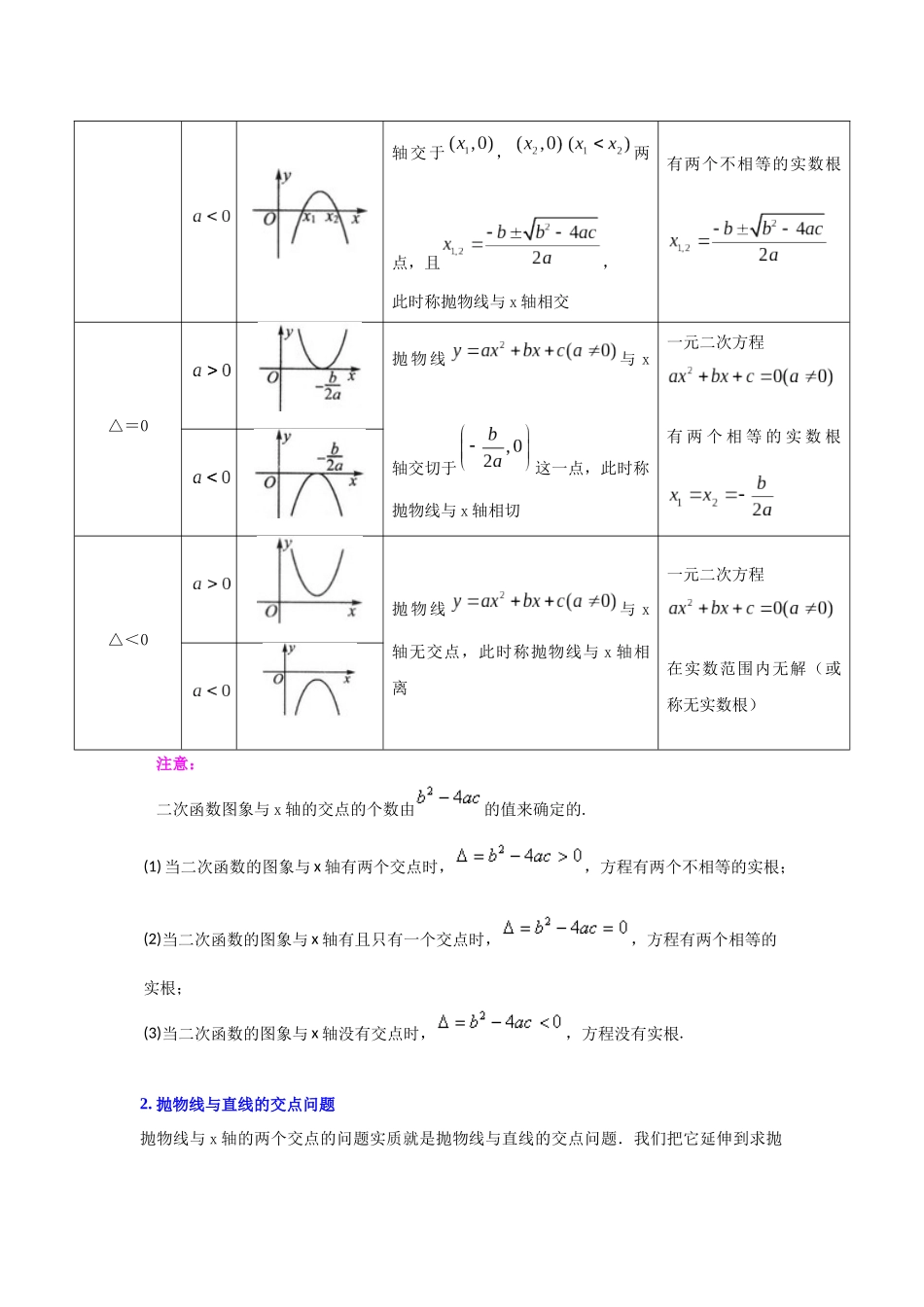
专题 22.1.6 二次函数与一元二次方程(知识解读 1)【直击考点】【学习目标】1. 会用图象法求一元二次方程的近似解;掌握二次函数与一元二次方程的关系;2. 经历探索验证二次函数与一元二次方程的关系的过程,学会用函数的观点去看方程和用数形结合的思想去解决问题. 【知识点梳理】考点 1 二次函数与一元二次方程的关系1.二次函数图象与 x 轴的交点情况决定一元二次方程根的情况 求二次函数(a≠0)的图象与 x 轴的交点坐标,就是令 y=0,求中 x 的值的问题.此时二次函数就转化为一元二次方程,因此一元二次方程根的个数决定了抛物线与 x 轴的交点的个数,它们的关系如下表:判别式二次函数一元二次方程图象与 x 轴的交点坐标根的情况△>0抛 物 线与 x一元二次方程轴交于,两点,且,此时称抛物线与 x 轴相交有两个不相等的实数根△=0抛 物 线与 x轴交切于这一点,此时称抛物线与 x 轴相切一元二次方程有 两 个 相 等 的 实 数 根△<0抛 物 线与 x轴无交点,此时称抛物线与 x 轴相离一元二次方程在实数范围内无解(或称无实数根) 注意: 二次函数图象与 x 轴的交点的个数由的值来确定的.(1)当二次函数的图象与 x 轴有两个交点时,,方程有两个不相等的实根;(2)当二次函数的图象与 x 轴有且只有一个交点时,,方程有两个相等的实根;(3)当二次函数的图象与 x 轴没有交点时,,方程没有实根.2. 抛物线与直线的交点问题抛物线与 x 轴的两个交点的问题实质就是抛物线与直线的交点问题.我们把它延伸到求抛物线(a≠0)与 y 轴交点和二次函数与一次函数的交点问题.抛物线(a≠0)与 y 轴的交点是(0,c).抛 物 线(a≠0) 与 一 次 函 数(k≠0) 的 交 点 个 数 由 方 程 组的解的个数决定.(1) 当方程组有两组不同的解时两函数图象有两个交点;(2) 当方程组有两组相同的解时两函数图象只有一个交点;(3) 当方程组无解时两函数图象没有交点. 总之,探究直线与抛物线的交点的问题,最终是讨论方程(组)的解的问题.注意:求两函数图象交点的问题主要运用转化思想,即将函数的交点问题转化为求方程组解的问题或者将求方程组的解的问题转化为求抛物线与直线的交点问题.考点 2 利用二次函数图象求一元二次方程的近似解 用图象法解一元二次方程的步骤:1.作二次函数的图象,由图象确定交点个数,即方程解的个数;2. 确定一元二次方程的根的取值范围.即确定抛...