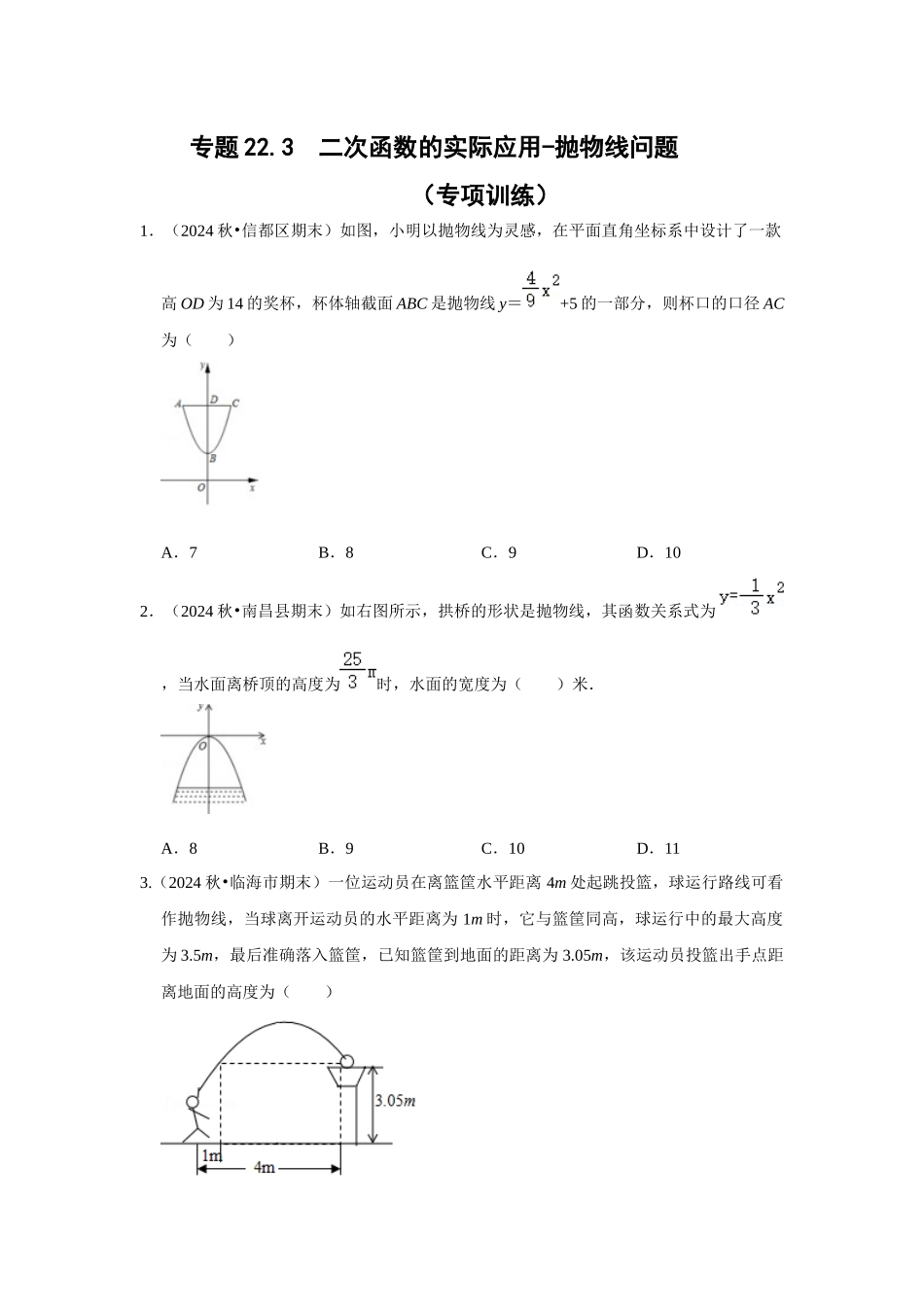
专题 22.3 二次函数的实际应用-抛物线问题(专项训练)1.(2024 秋•信都区期末)如图,小明以抛物线为灵感,在平面直角坐标系中设计了一款高 OD 为 14 的奖杯,杯体轴截面 ABC 是抛物线 y=+5 的一部分,则杯口的口径 AC为( )A.7B.8C.9D.102.(2024 秋•南昌县期末)如右图所示,拱桥的形状是抛物线,其函数关系式为,当水面离桥顶的高度为时,水面的宽度为( )米.A.8B.9C.10D.113.(2024 秋•临海市期末)一位运动员在离篮筐水平距离 4m 处起跳投篮,球运行路线可看作抛物线,当球离开运动员的水平距离为 1m 时,它与篮筐同高,球运行中的最大高度为 3.5m,最后准确落入篮筐,已知篮筐到地面的距离为 3.05m,该运动员投篮出手点距离地面的高度为( )A.1.5 mB.2mC.2.25 mD.2.5 m4.(2024 秋•峄城区期末)从地面竖直向上抛出一小球,小球的高度 h(单位:m)与小球运动时间 t(单位:s)之间的函数关系如图所示,下列结论:① 小球在空中经过的路程是 40m;② 小球抛出 3 秒后,速度越来越快;③ 小球抛出 3 秒时速度为 0;④ 小球的高度 h=30m 时,t=1.5s.其中正确的是( )A.①④B.①②C.②③D.②③④5.(2025•江西开学)如图,从m 高的某建筑物窗口 A 用水管向外给公园草坪喷水,喷出的水呈抛物线状(抛物线所在的平面与墙面垂直),已知喷出的水(抛物线)的最高点 M 离墙 1m 时最大高度为 8m,求水流落地点 B 离墙的距离 OB.6.(2025•浦江县模拟)把一个抛物线形的拱形桥洞放在如图所示的直角坐标系中,桥洞离水面的最大高度为 4m,跨度为 12m.(1)求这条抛物线的解析式.(2)一艘宽为 4 米,高出水面 3 米的货船,能否从桥下通过?并说明理由.7.(2025•丰台区一模)某公园在人工湖里安装一个喷泉,在湖心处竖直安装一根水管,在水管的顶端安一个喷水头,水柱从喷水头喷出到落于湖面的路径形状可以看作是抛物线的一部分.若记水柱上某一位置与水管的水平距离为 d 米,与湖面的垂直高度为 h米.下面的表中记录了 d 与 h 的五组数据:d(米)01234h(米)0.51.251.51.250.5根据上述信息,解决以下问题:(1)在下面网格(图 1)中建立适当的平面直角坐标系,并根据表中所给数据画出表示h 与 d 函数关系的图象;(2)若水柱最高点距离湖面的高度为 m 米,则 m= ;(3)现公园想通过喷泉设立新的游玩项目,准备通过只调节水...