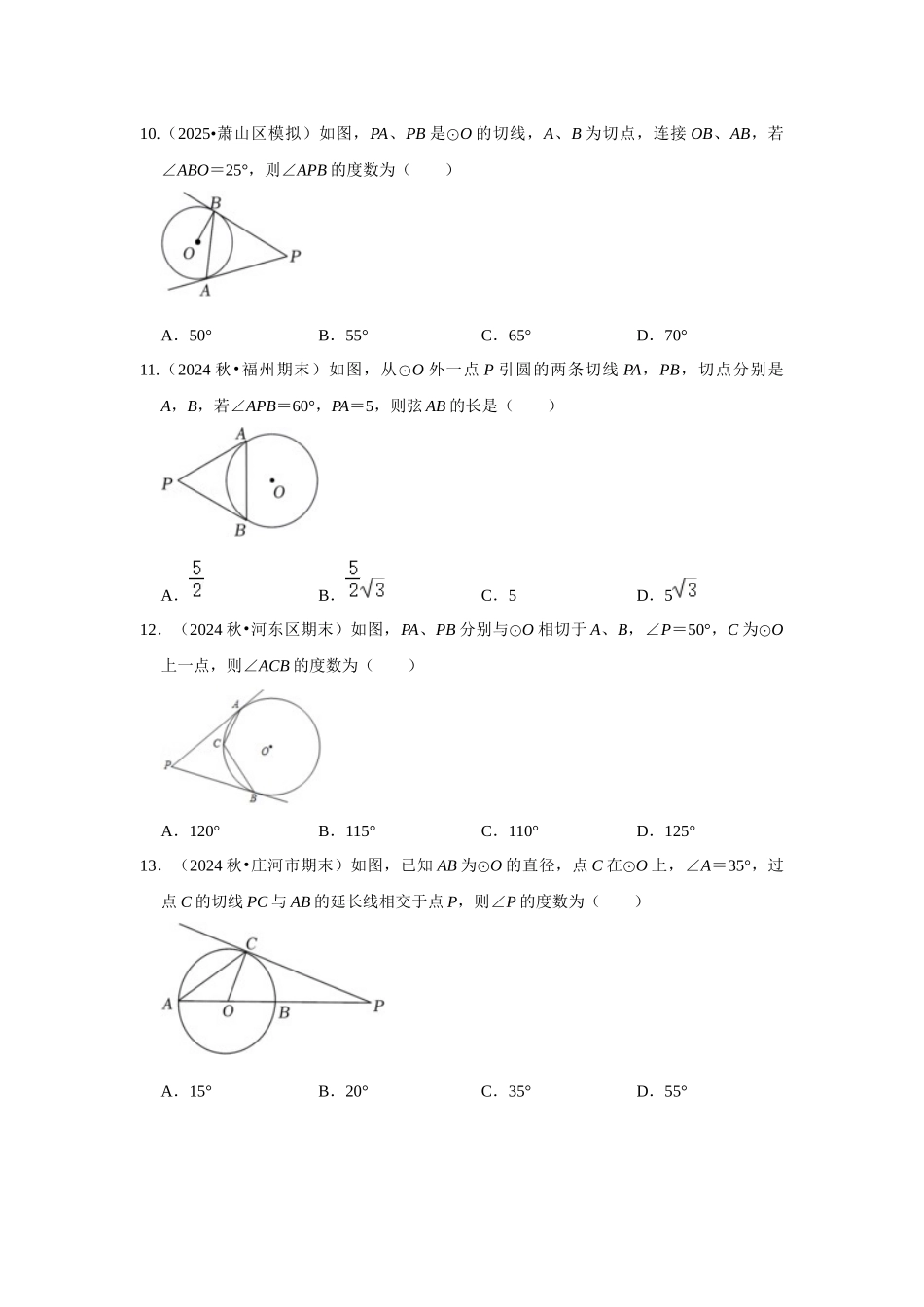
专题 24.2.2 直线与圆的位置关系(专项训练)1.(2025•东明县一模)已知平面内有⊙O 和点 A,B,若⊙O 的半径为 2cm,线段 OA=3cm,OB=2cm,则直线 AB 与⊙O 的位置关系为( )A.相交B.相切C.相交或相切D.相离2.(2024 秋•招远市期末)已知⊙O 的半径为 4cm,圆心 O 到直线 l 的距离为 3cm,则直线 l 与⊙O 的位置关系为( )A.相交B.相切C.相离D.无法确定3.(2024 秋•平罗县期末)在平面直角坐标系中,以点(﹣2,3)为圆心,半径为 3 的圆一定( )A.与 x 轴相切,与 y 轴相切B.与 x 轴相切,与 y 轴相交C.与 x 轴相交,与 y 轴相切D.与 x 轴相交,与 y 轴相交4.(2024 秋•武汉期末)直角△ABC,∠BAC=90°,AB=8,AC=6,以 A 为圆心,4.8 长度为半径的圆与直线 BC 的公共点的个数为( )A.0B.1C.2D.不能确定5.(2024 秋•金安区校级期末)如图所示,直线 y=x2﹣ 与 x 轴、y 轴分别交于 M,N 两点 , ⊙ O 的 半 径 为 1 , 将 ⊙ O 以 每 秒 1 个 单 位 的 速 度 向 右 作 平 移 运 动 , 当 移 动 s 时,直线 MN 恰好与圆 O 相切.6.(2025•莆田模拟)如图,AB 是⊙O 的直径,BC 是⊙O 的切线,若∠ACB=55°,则∠BAC 的大小为( )A.25°B.35°C.45°D.55°7.(2024 秋•邗江区期末)如图,AB 是⊙O 的直径,点 D 在 AB 的延长线上,DC 切⊙O 于点 C,若∠A=20°,则∠D 等于( )A.20°B.30°C.50°D.40°8.(2024 秋•莆田期末)如图,AB、AC、BD 分别切⊙O 于点 P、C、D.若 AB=5,AC=3,则 BD 的长是( )A.4B.3C.2D.19.(2024 秋•忠县期末)如图,BC 与⊙O 相切于点 C,AB 经过⊙O 的圆心与⊙O 交于 D,若∠B=40°,则∠A=( )A.20°B.25°C.30°D.35°10.(2025•萧山区模拟)如图,PA、PB 是⊙O 的切线,A、B 为切点,连接 OB、AB,若∠ABO=25°,则∠APB 的度数为( )A.50°B.55°C.65°D.70°11.(2024 秋•福州期末)如图,从⊙O 外一点 P 引圆的两条切线 PA,PB,切点分别是A,B,若∠APB=60°,PA=5,则弦 AB 的长是( )A.B.C.5D.512.(2024 秋•河东区期末)如图,PA、PB 分别与⊙O 相切于 A、B,∠P=50°,C 为⊙O上一点,则∠ACB 的度数为( )A.120°B.115°C.110°D.125°13...