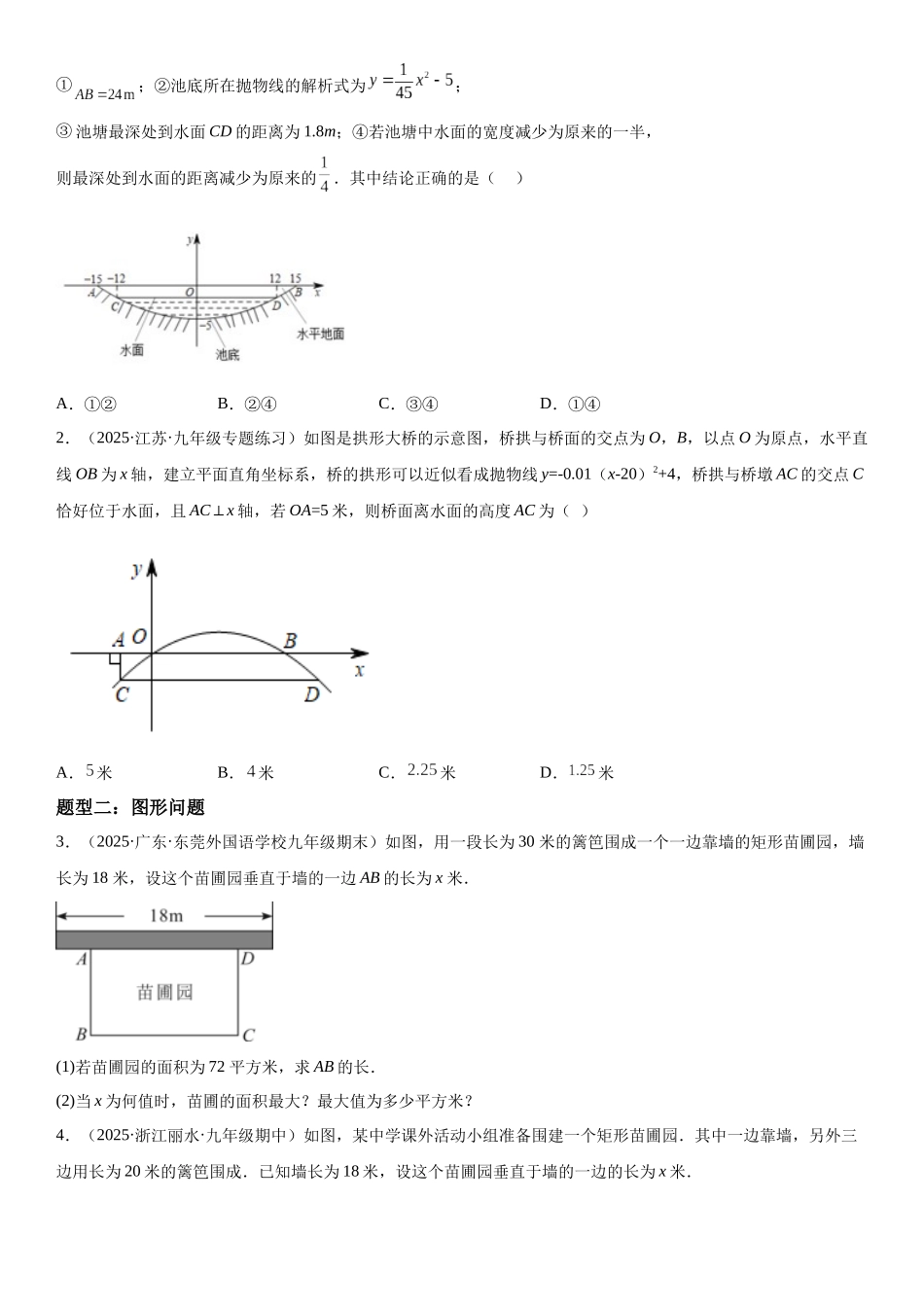
22.3 实际问题与二次函数考点一.利用二次函数解决利润问题利润问题主要涉及两个等量关系:利润=售价-进价;总利润=单件商品的利润×销售量.在日常生活中,经常遇到求最大利润、最高产量等问题,在解答此类问题时,应建立函数模型,把它们转化为求函数的最值问题,然后列出相应的函数解析式,从而解决问题.建立二次函数模型解决实际问题的一般步骤:(1)审题;(2)找出题中的已知量和未知量;(3)用一个未知量表示题中的其他未知量;(4)找出等量关系并列出函数解析式;(5)利用二次函数的图象及性质去分析、解决实际问题.考点二.利用二次函数求图形面积的最值(1)二次函数的最值:一般地,当 a>0(a<0)时,抛物线 y=ax2+bx+c 的顶点是最低(最高)点,也就是说,当 x=时,二次函数 y=ax2+bx+c 有最小(最大)值,最小(最大)值为.(2)应用二次函数解决实际问题的基本思路:① 理解题意;②分析问题中的变量和常量以及它们之间的关系;③用函数解析式表示它们之间的关系;④用数学方法求解;⑤检验结果的合理性. 考点三.利用二次函数解决抛物线形问题在实际生活中,如拱门、桥洞等问题,都可以通过建立二次函数模型来解答.在解答此类问题的过程中,要运用数形结合思想和函数思想,在图形上先建立合适的平面直角坐标系,再根据题意设出适当的函数解析式,然后由已知点的坐标,利用待定系数法求出函数解析式,最后根据函数解析式来分析解答问题.题型一:拱桥问题1.(2023·河北·九年级专题练习)某池塘的截面如图所示,池底呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:m).有下列结论:①;②池底所在抛物线的解析式为;③ 池塘最深处到水面 CD 的距离为 1.8m;④若池塘中水面的宽度减少为原来的一半,则最深处到水面的距离减少为原来的.其中结论正确的是( )A.①②B.②④C.③④D.①④2.(2025·江苏·九年级专题练习)如图是拱形大桥的示意图,桥拱与桥面的交点为 O,B,以点 O 为原点,水平直线 OB 为 x 轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线 y=-0.01(x-20)2+4,桥拱与桥墩 AC 的交点 C恰好位于水面,且 AC⊥x 轴,若 OA=5 米,则桥面离水面的高度 AC 为( )A. 米B.米C.米D.米题型二:图形问题3.(2025·广东·东莞外国语学校九年级期末)如图,用一段长为 30 米的篱笆围成一个一边靠墙的矩形苗圃园,墙长为 18 米,设这个苗圃园垂直...