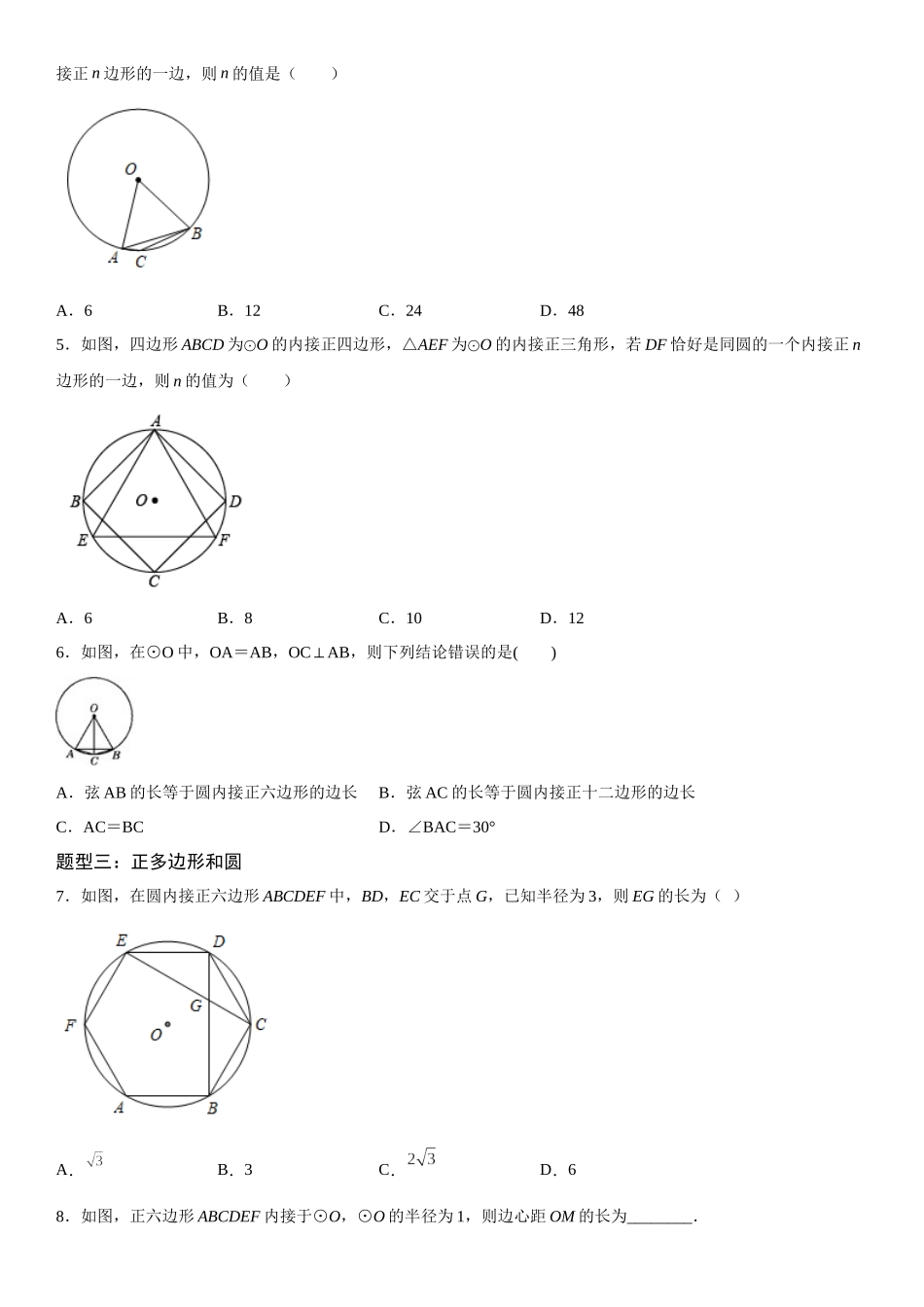
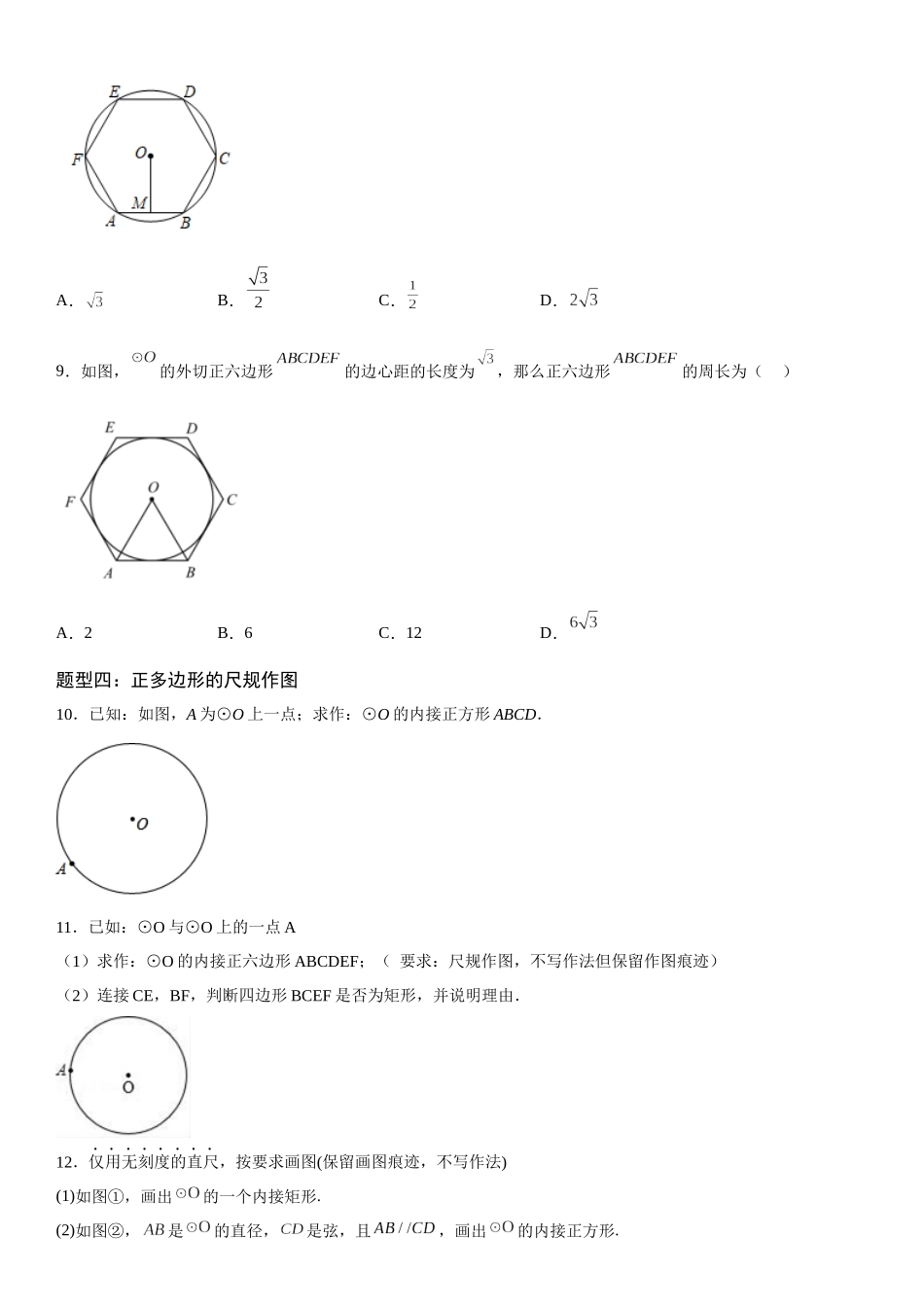
24.3 正多边形和圆考点一:正多边形及有关概念只要把一个圆分成 相等 的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的 外接 圆.一个正多边形的外接圆的 圆心 叫作这个正多边形的中心,外接圆的 半径 叫作这个正多边形的半径;正多边形每一边所对的 圆心角 叫作正多边形的中心角;中心到正多边形的一边的距离叫做正多边形的 边心 距 .考点二:正多边形的有关计算一般地,正 n 边形的一个内角的度数为 ,中心角的度数等于 ;正多边形的中心角与外角的大小 相等 .题型一:正多边形的中心角1.在圆内接正六边形 ABCDEF 中,正六边形的边长为 2,则这个正六边形的中心角和边心距分别是( )A.30°,1B.45°,2C.60°,D.120°,42.如图,正六边形内接于,点 M 在上,则的度数为( )A.B.C.D.3.如图,正六边形与正方形有两个顶点重合,且中心都是点 O.若∠AOB 是某正 n 边形的一个外角,则 n 的值为( )A.16B.12C.10D.8题型二:求正多边形的边数4.如图,边 AB 是⊙O 内接正六边形的一边,点 C 在上,且 BC 是⊙O 内接正八边形的一边,若 AC 是⊙O 内接正 n 边形的一边,则 n 的值是( )A.6B.12C.24D.485.如图,四边形 ABCD 为⊙O 的内接正四边形,△AEF 为⊙O 的内接正三角形,若 DF 恰好是同圆的一个内接正 n边形的一边,则 n 的值为( )A.6B.8C.10D.126.如图,在⊙O 中,OA=AB,OCAB⊥,则下列结论错误的是( )A.弦 AB 的长等于圆内接正六边形的边长B.弦 AC 的长等于圆内接正十二边形的边长C.AC=BCD.∠BAC=30°题型三:正多边形和圆7.如图,在圆内接正六边形 ABCDEF 中,BD,EC 交于点 G,已知半径为 3,则 EG 的长为( )A.B.3C.D.68.如图,正六边形 ABCDEF 内接于⊙O,⊙O 的半径为 1,则边心距 OM 的长为________.A.B.C.D.9.如图,的外切正六边形的边心距的长度为,那么正六边形的周长为( )A.2B.6C.12D.题型四:正多边形的尺规作图10.已知:如图,A 为⊙O 上一点;求作:⊙O 的内接正方形 ABCD.11.已如:⊙O 与⊙O 上的一点 A(1)求作:⊙O 的内接正六边形 ABCDEF;( 要求:尺规作图,不写作法但保留作图痕迹)(2)连接 CE,BF,判断四边形 BCEF 是否为矩形,并说明理由.12.仅用无刻度的直尺,按要求画图(保留画图痕迹,不写作法)(1)如图①,画出的一个内接...