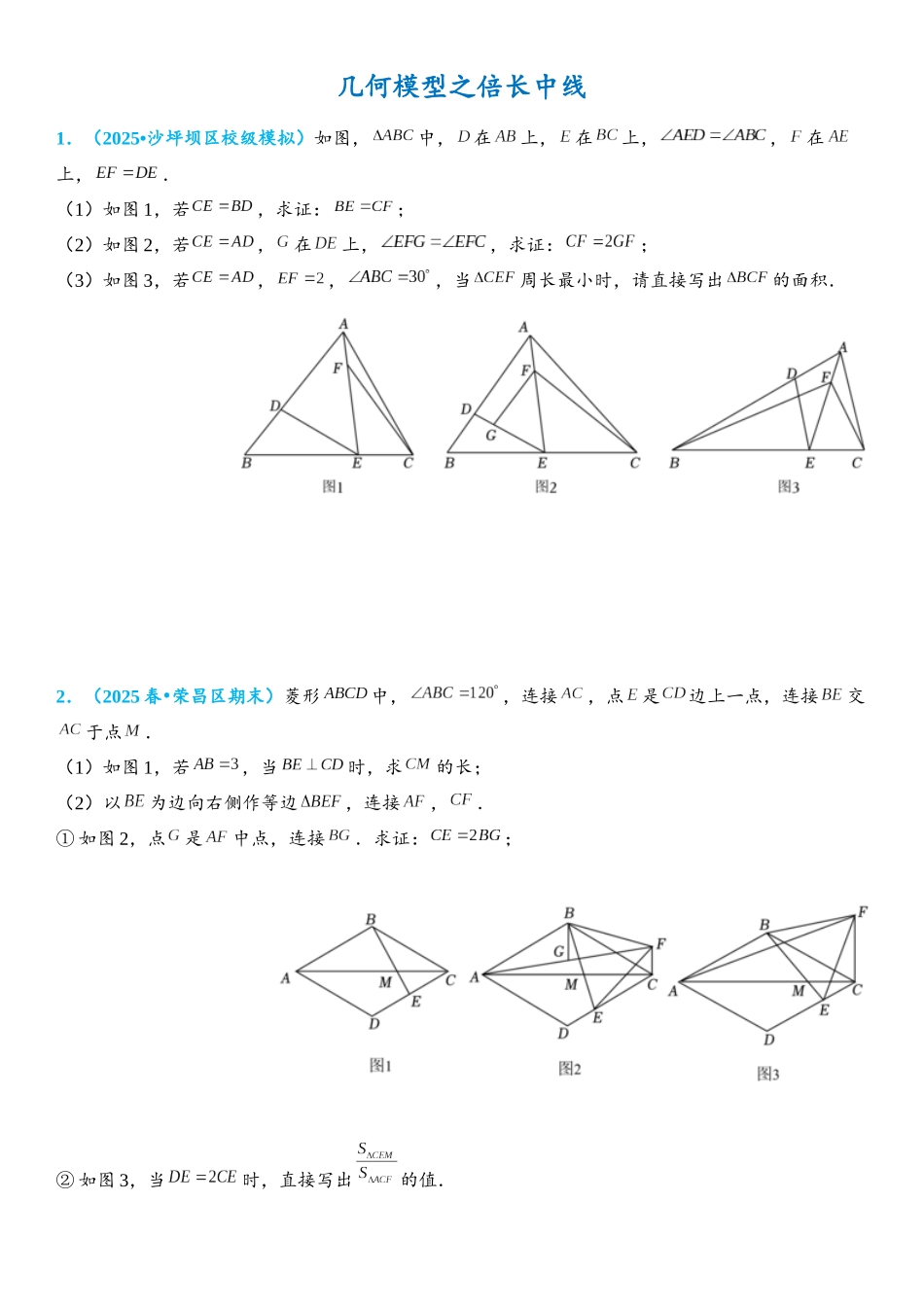
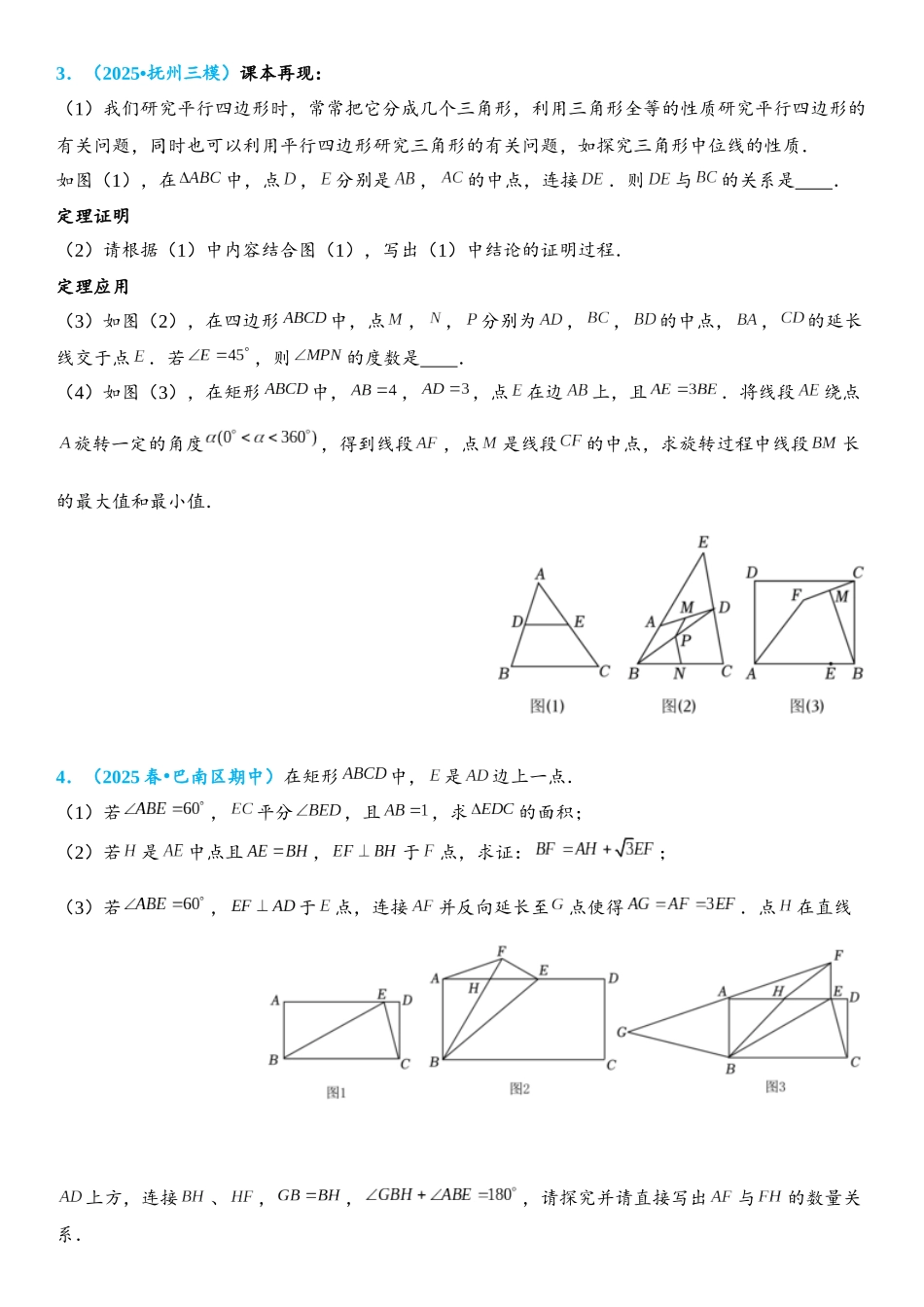
几何模型之倍长中线1.(2025•沙坪坝区校级模拟)如图,中,在上,在上,,在上,.(1)如图 1,若,求证:;(2)如图 2,若,在上,,求证:;(3)如图 3,若,,,当周长最小时,请直接写出的面积.2.(2025 春 荣昌区期末)•菱形中,,连接,点是边上一点,连接交于点.(1)如图 1,若,当时,求的长;(2)以为边向右侧作等边,连接,.① 如图 2,点是中点,连接.求证:;② 如图 3,当时,直接写出的值.3.(2025•抚州三模)课本再现:(1)我们研究平行四边形时,常常把它分成几个三角形,利用三角形全等的性质研究平行四边形的有关问题,同时也可以利用平行四边形研究三角形的有关问题,如探究三角形中位线的性质.如图(1),在中,点,分别是,的中点,连接.则与的关系是 .定理证明(2)请根据(1)中内容结合图(1),写出(1)中结论的证明过程.定理应用(3)如图(2),在四边形中,点,,分别为,,的中点,,的延长线交于点.若,则的度数是 .(4)如图(3),在矩形中,,,点在边上,且.将线段绕点旋转一定的角度,得到线段,点是线段的中点,求旋转过程中线段长的最大值和最小值.4.(2025 春 巴南区期中)•在矩形中,是边上一点.(1)若,平分,且,求的面积;(2)若是中点且,于点,求证:;(3)若,于点,连接并反向延长至点使得.点在直线上方,连接、,,,请探究并请直接写出与的数量关系.5.(2025 春 碑林区校级期中)•为了进一步探究三角形中线的作用,数学兴趣小组合作交流时,小丽在组内做了如下尝试:如图 1,在中,是边上的中线,延长到,使,连接.【探究发现】(1)图 1 中与的数量关系是 ,位置关系是 ;【初步应用】(2)如图 2,在中,若,,求边上的中线的取值范围.(提示:不等式的两边都乘或除以同一个正数,不等号的方向不变.例如:若,则.【探究提升】(3)如图 3,是的中线,过点分别向外作、,使得,,延长交于点,判断线段与的数量关系和位置关系,请说明理由.6.(2025 秋 南沙区校级期末)•如图,在中,点是的中点,分别以,为腰向外作等腰三角形和等腰三角形,其中,,,,,连接.(1)请写出与的数量关系,并说明理由.(2)延长交于点,求的度数.7.(2025•蜀山区校级一模)如图,在中,,,于点,点是的中点,连接.(1)若,,求的长;(2)求证:;(3)求证:.8.(2025 秋 东城区期末)•如图,在等边三角形中,点为内一点,连...