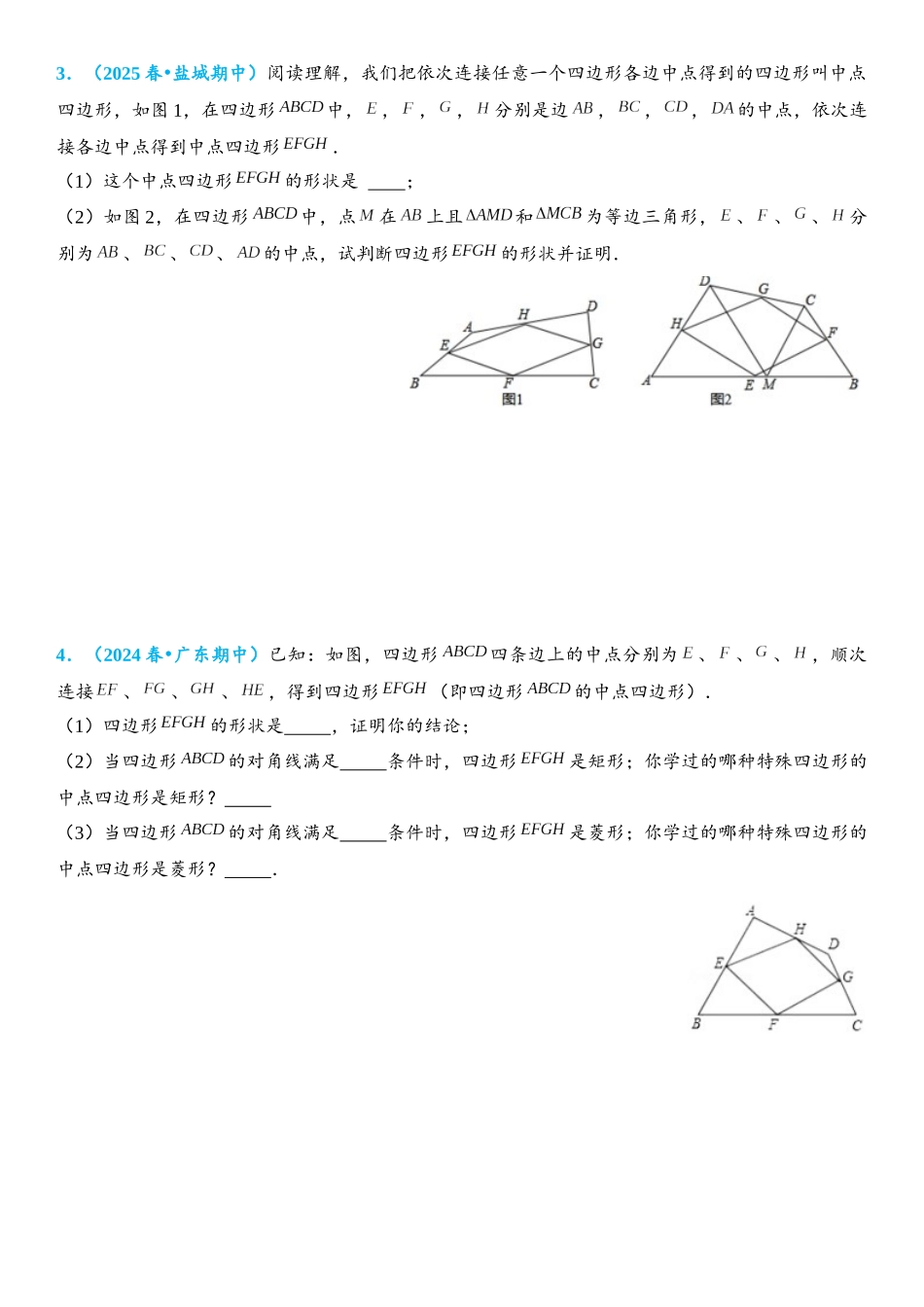
中点四边形1．（2025 春 怀仁市期中）•已知：如图，四边形四条边上的中点分别为、、、，顺次连接、、、，得到四边形（即四边形的中点四边形）．（1）四边形的形状是 ，证明你的结论．（2）当四边形的对角线满足 条件时，四边形是矩形．（3）你学过的哪种特殊四边形的中点四边形是菱形
．2．（2024 春 建湖县期中）•阅读理解我们把依次连接任意一个四边形各边中点得到的四边形叫中点四边形．如图 1，在四边形中，，，，分别是边，，，的中点，依次连接各边中点得到中点四边形．问题解决（1）判断图 1 中的中点四边形的形状，并说明理由；（2）当图 1 中的四边形的对角线添加条件 时，这个中点四边形是正方形．拓展延伸（3）如图 2，在四边形中，点在上且和为等边三角形，、、、分别为、、、的中点，试判断四边形的形状，并证明你的结论．3．（2025 春 盐城期中）•阅读理解，我们把依次连接任意一个四边形各边中点得到的四边形叫中点四边形，如图 1，在四边形中，，，，分别是边，，，的中点，依次连接各边中点得到中点四边形．（1）这个中点四边形的形状是 ；（2）如图 2，在四边形中，点在上且和为等边三角形，、、、分别为、、、的中点，试判断四边形的形状并证明．4．（2024 春 广东期中）•已知：如图，四边形四条边上的中点分别为、、、，顺次连接、、、，得到四边形（即四边形的中点四边形）．（1）四边形的形状是 ，证明你的结论；（2）当四边形的对角线满足 条件时，四边形是矩形；你学过的哪种特殊四边形的中点四边形是矩形
（3）当四边形的对角线满足 条件时，四边形是菱形；你学过的哪种特殊四边形的中点四边形是菱形
．5．（2024 春 饶平县期末）•我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形，如图，、、、分别是四边形各边的中点，可证中点四边形是平行四边形，如果我们对四边形的对角线与添加一定的
