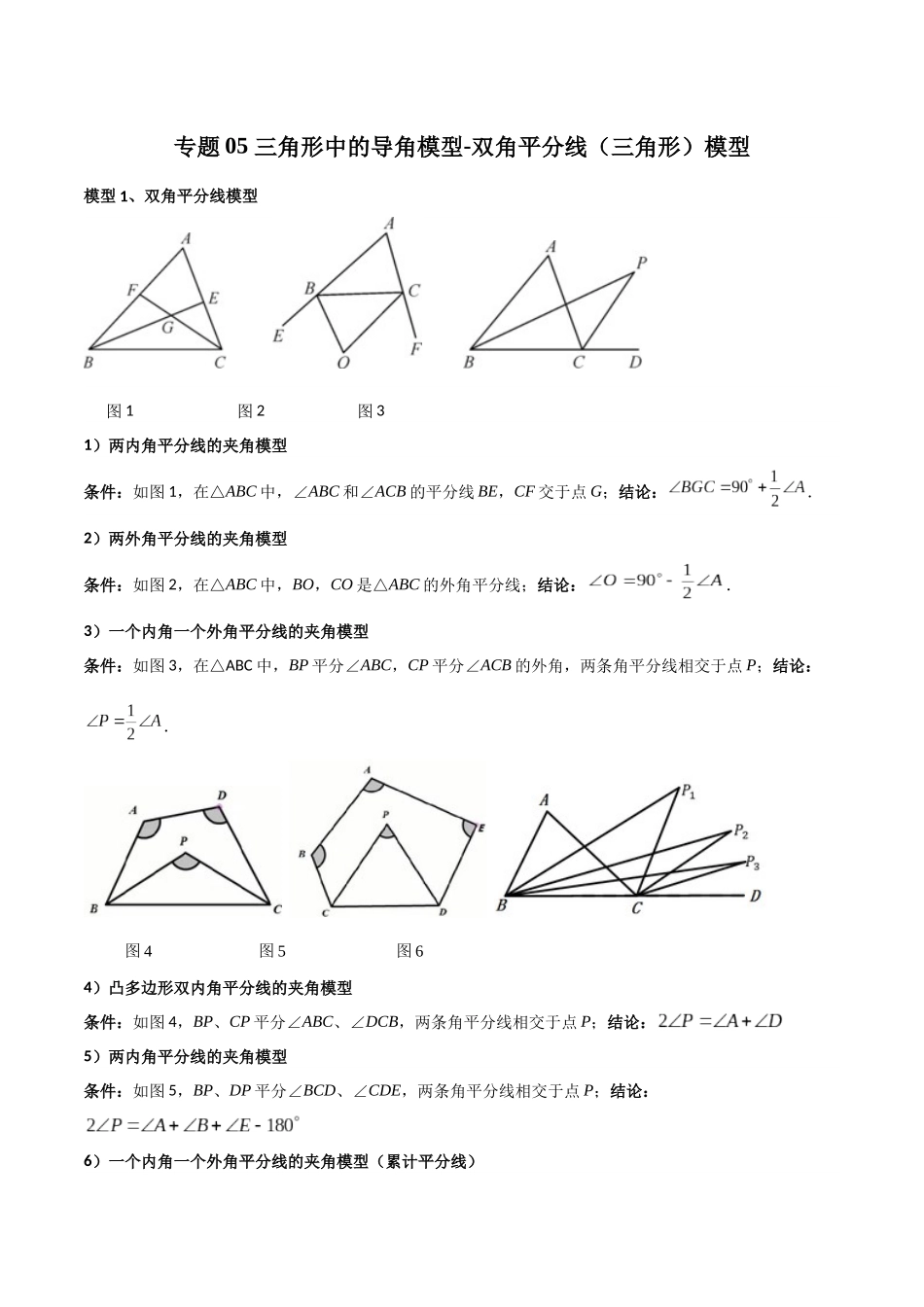
专题 05 三角形中的导角模型-双角平分线(三角形)模型模型 1、双角平分线模型 图 1 图 2 图 3 1)两内角平分线的夹角模型条件:如图 1,在△ABC 中,∠ABC 和∠ACB 的平分线 BE,CF 交于点 G;结论:.2)两外角平分线的夹角模型条件:如图 2,在△ABC 中,BO,CO 是△ABC 的外角平分线;结论:.3)一个内角一个外角平分线的夹角模型条件:如图 3,在△ABC 中,BP 平分∠ABC,CP 平分∠ACB 的外角,两条角平分线相交于点 P;结论:. 图 4 图 5 图 64)凸多边形双内角平分线的夹角模型条件:如图 4,BP、CP 平分∠ABC、∠DCB,两条角平分线相交于点 P;结论:5)两内角平分线的夹角模型条件:如图 5,BP、DP 平分∠BCD、∠CDE,两条角平分线相交于点 P;结论:6)一个内角一个外角平分线的夹角模型(累计平分线)条件:如图 6,,的平分线相交于点,的平分线相交于点,,的平分线相交于点……以此类推;结论:的度数是.7)旁心模型旁心:三角形的一条内角平分线与其他两个角的外角平分线交于一点EDCBAh1h2h3EDCBA条件:如图,BD 平分∠ABC,CD 平分∠ACB 的外角,两条角平分线相交于点 D;结论:AD 平分∠CAD例 1.(2025 秋·安徽阜阳·八年级统考期中)如图,在中,点是内一点,且点到三边的距离相等,若,则 .例 2.(2025·湖北十堰·八年级统考期末)如图,在五边形 ABCDE 中,,DP,CP 分别平分,,则的度数是 .例 3.(2025·山东济南·校考模拟预测)如图 1,在△ABC 中,∠BAC 的平分线 AD 与∠BCA 的平分线 CE交于点 O.(1)求证:∠AOC=90°+∠ABC;(2)当∠ABC=90°时,且 AO=3OD(如图 2),判断线段AE,CD,AC 之间的数量关系,并加以证明.例 4.(2025 秋·成都市·八年级专题练习)如图,在中,,三角形两外角的角平分线交于点E,则 .例 5.(2025·湖北·八年级专题练习)如图,已知在中,、的外角平分线相交于点,若,,求的度数.例 6.(2025·辽宁葫芦岛·八年级统考期中)如图,CD、BD 分别平分∠ACE、∠ABC,∠A=70°,则∠BDC=( )A.35°B.25°C.70°D.60°例 7.(2025 秋·八年级课时练习)如图,和分别是的内角平分线和外角平分线,是的平分线,是的平分线,是的平分线,是的平分线,……以此类推,若,则 .例 8.(2025 春·成都市七年级课时练习)如图在△ABC 中,BO,CO 分别平分∠ABC,∠ACB,交于 O,CE为外角...