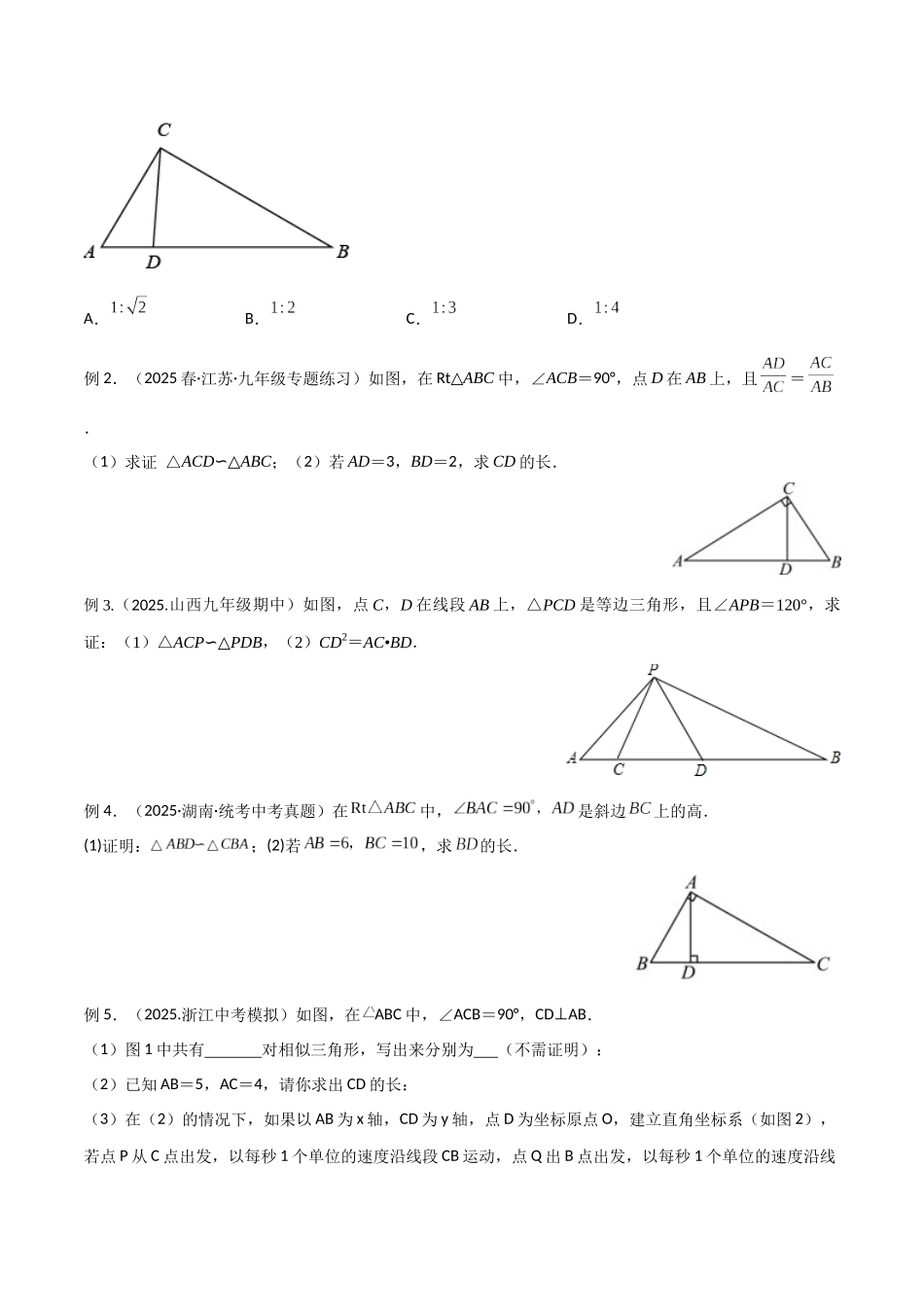
专题 20. 相似三角形重要模型--母子型(共边共角模型)相似三角形是初中几何中的重要的内容,常常与其它知识点结合以综合题的形式呈现,其变化很多,是中考的常考题型。在相似三角形中存在众多的相似模型,其中“母子型”相似模型应用较为广泛,深入理解模型内涵,灵活运用相关结论可以显著提高解题效率,本专题重点讲解相似三角形的“母子”模型。母子相似证明题一般思路方法:① 由线段乘积相等转化成线段比例式相等;② 分子和分子组成一个三角形、分母和分母组成一个三角形;③ 第②步成立,直接从证这两个三角形相似,逆向证明到线段乘积相等;④ 第②步不成立,则选择替换掉线段比例式中的个别线段,之后再重复第③步。模型 1.“母子”模型(共边角模型)【模型解读与图示】“母子”模型的图形(通常有一个公共顶点和另外一个不是公共的顶点,由于小三角形寓于大三角形中,恰似子依母怀),也是有一个“公共角”,再有一个角相等或夹这个公共角的两边对应成比例就可以判定这两个三角形相似. 图 1 图 2 图 3 图 41)“母子”模型(斜射影模型)条件:如图 1,∠C=∠ABD; 结论:△ABD∽△ACB,AB2=AD·AC.2)双垂直模型(射影模型)条件:如图 2,∠ACB=90o,CD⊥AB;结论:△ACD∽△ABC∽△CBD;CA2=AD·AB,BC2=BD·BA,CD2=DA·DB.3)“母子”模型(变形)条件:如图 3,∠D=∠CAE,AB=AC; 结论:△ABD∽△ECA;4)共边模型条件:如图 1,在四边形中,对角线平分,,结论:;例 1.(2025·贵州贵阳·中考真题)如图,在中,是边上的点,,,则与的周长比是( )A.B.C.D.例 2.(2025 春·江苏·九年级专题练习)如图,在 Rt△ABC 中,∠ACB=90°,点 D 在 AB 上,且=.(1)求证 △ACD∽△ABC;(2)若 AD=3,BD=2,求 CD 的长.例 3.(2025.山西九年级期中)如图,点 C,D 在线段 AB 上,△PCD 是等边三角形,且∠APB=120°,求证:(1)△ACP∽△PDB,(2)CD2=AC•BD.例 4.(2025·湖南·统考中考真题)在中,是斜边上的高.(1)证明:;(2)若,求的长. 例 5.(2025.浙江中考模拟)如图,在ABC 中,∠ACB=90°,CDAB⊥.(1)图 1 中共有 对相似三角形,写出来分别为 (不需证明):(2)已知 AB=5,AC=4,请你求出 CD 的长:(3)在(2)的情况下,如果以 AB 为 x 轴,CD 为 y 轴,点 D 为坐标原点 O,建立直角坐标系(如图 2),若点 P 从 C 点...