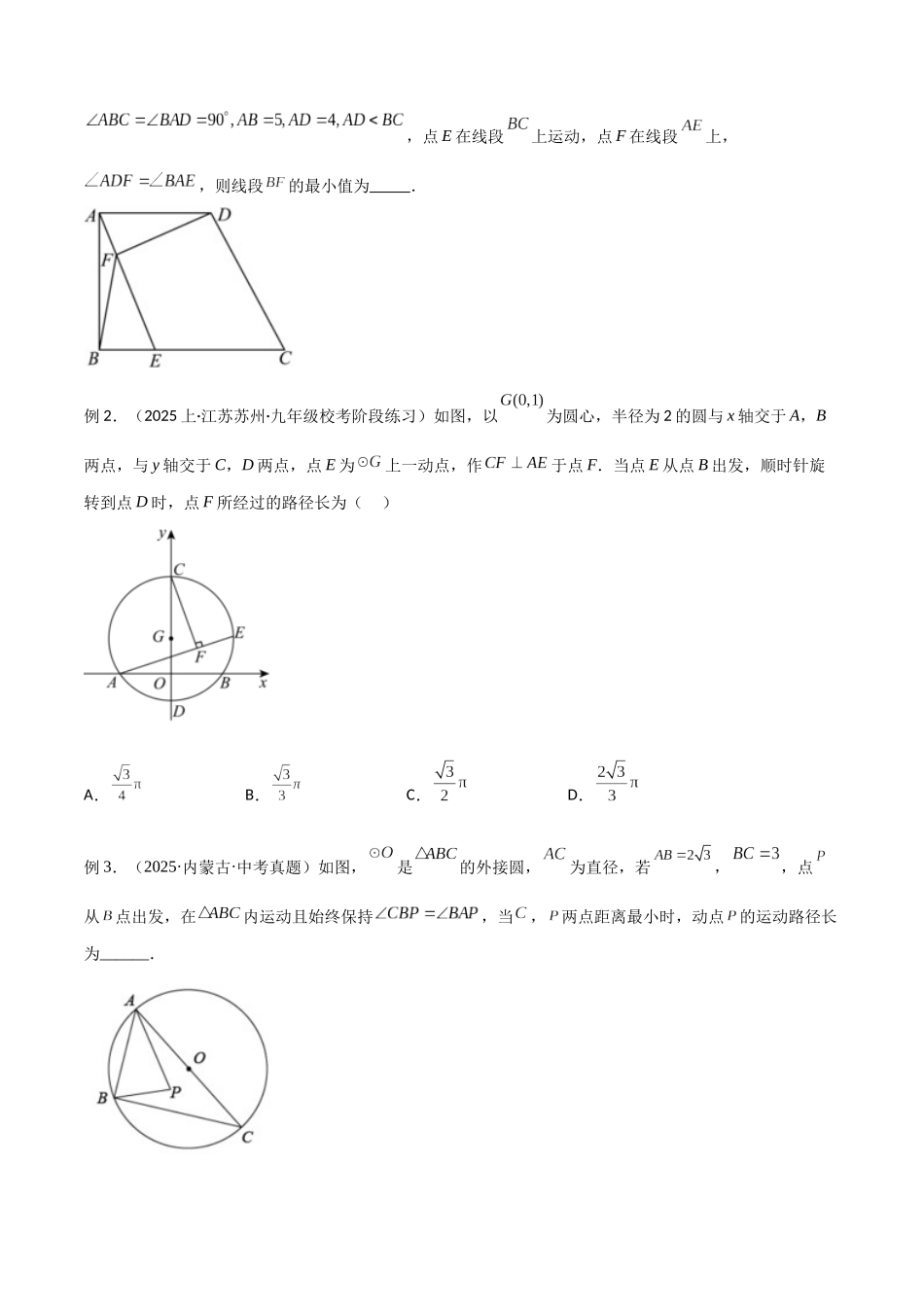
专题 32 圆中的重要模型之隐圆模型隐圆是各地中考选择题和填空题、甚至解答题中常考题,题目常以动态问题出现,有点、线的运动,或者图形的折叠、旋转等,大部分学生拿到题基本没有思路,更谈不上如何解答。隐圆常见形式:动点定长、定弦对直角、定弦对定角、四点共圆等,上述四种动态问题的轨迹是圆。题目具体表现为折叠问题、旋转问题、角度不变问题等,此类问题综合性强,隐蔽性强,很容易造成同学们的丢分。本专题就隐圆模型的相关问题进行梳理及对应试题分析,方便掌握。模型 1、动点定长模型(圆的定义)若 P 为动点,且 AB=AC=AP,则 B、C、P 三点共圆,A 圆心,AB 半径 圆的定义:平面内到定点的距离等于定值的所有点构成的集合.寻找隐圆技巧:若动点到平面内某定点的距离始终为定值,则其轨迹是圆或圆弧.例 1.(2025·山东泰安·统考中考真题)如图,在平面直角坐标系中,的一条直角边在 x 轴上,点 A 的坐标为;中,,连接,点 M 是中点,连接.将以点 O 为旋转中心按顺时针方向旋转,在旋转过程中,线段的最小值是( ) A.3B.C.D.2例 2.(2025·广东清远·统考三模)如图,在,,E 为边上的任意一点,把沿折叠,得到,连接.若,,则的最小值为 .例 3.(2025·北京市·九年级专题练习)如图,四边形中,、分别是,的中垂线,,,则___,___.例 4.(2025 上·江苏无锡·九年级校联考期中)如图,正方形 ABCD 中,,E 是的中点.以点 C为圆心,长为半径画圆,点 P 是上一动点,点 F 是边上一动点,连接,若点 Q 是的中点,连接,,则的最小值为 .模型 2、定边对直角模型(直角对直径)固定线段 AB 所对动角∠C 恒为 90°,则 A、B、C 三点共圆,AB 为直径 寻找隐圆技巧:一条定边所对的角始终为直角,则直角顶点轨迹是以定边为直径的圆或圆弧.例 1.(2025·山东·统考中考真题)如图,在四边形中,,点 E 在线段上运动,点 F 在线段上,,则线段的最小值为 . 例 2.(2025 上·江苏苏州·九年级校考阶段练习)如图,以为圆心,半径为 2 的圆与 x 轴交于 A,B两点,与 y 轴交于 C,D 两点,点 E 为上一动点,作于点 F.当点 E 从点 B 出发,顺时针旋转到点 D 时,点 F 所经过的路径长为( ) A.B.C.D.例 3.(2025·内蒙古·中考真题)如图,是的外接圆,为直径,若,,点从点出发,在内运动且始终保持,当,两点距离最小时,动点的...