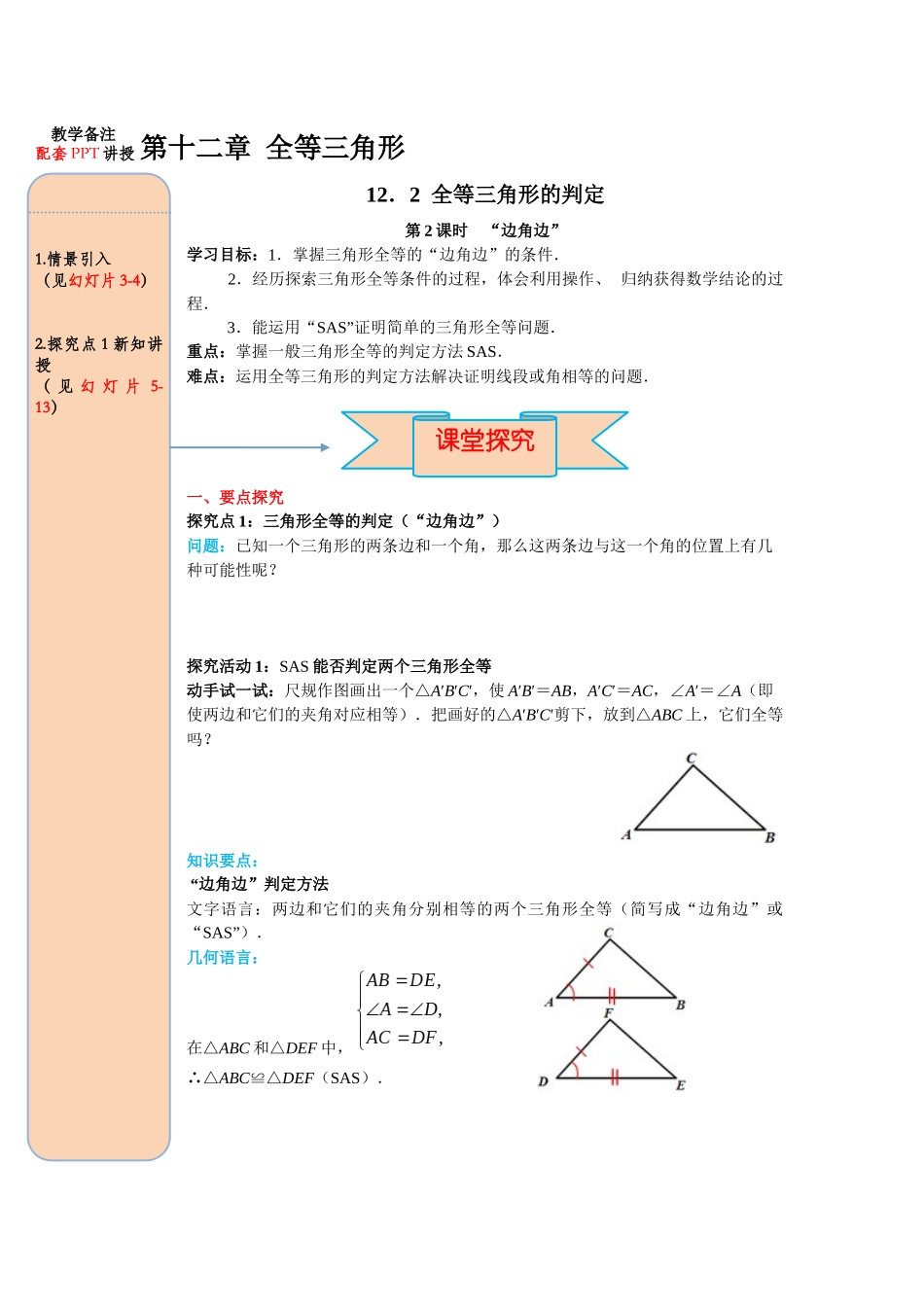
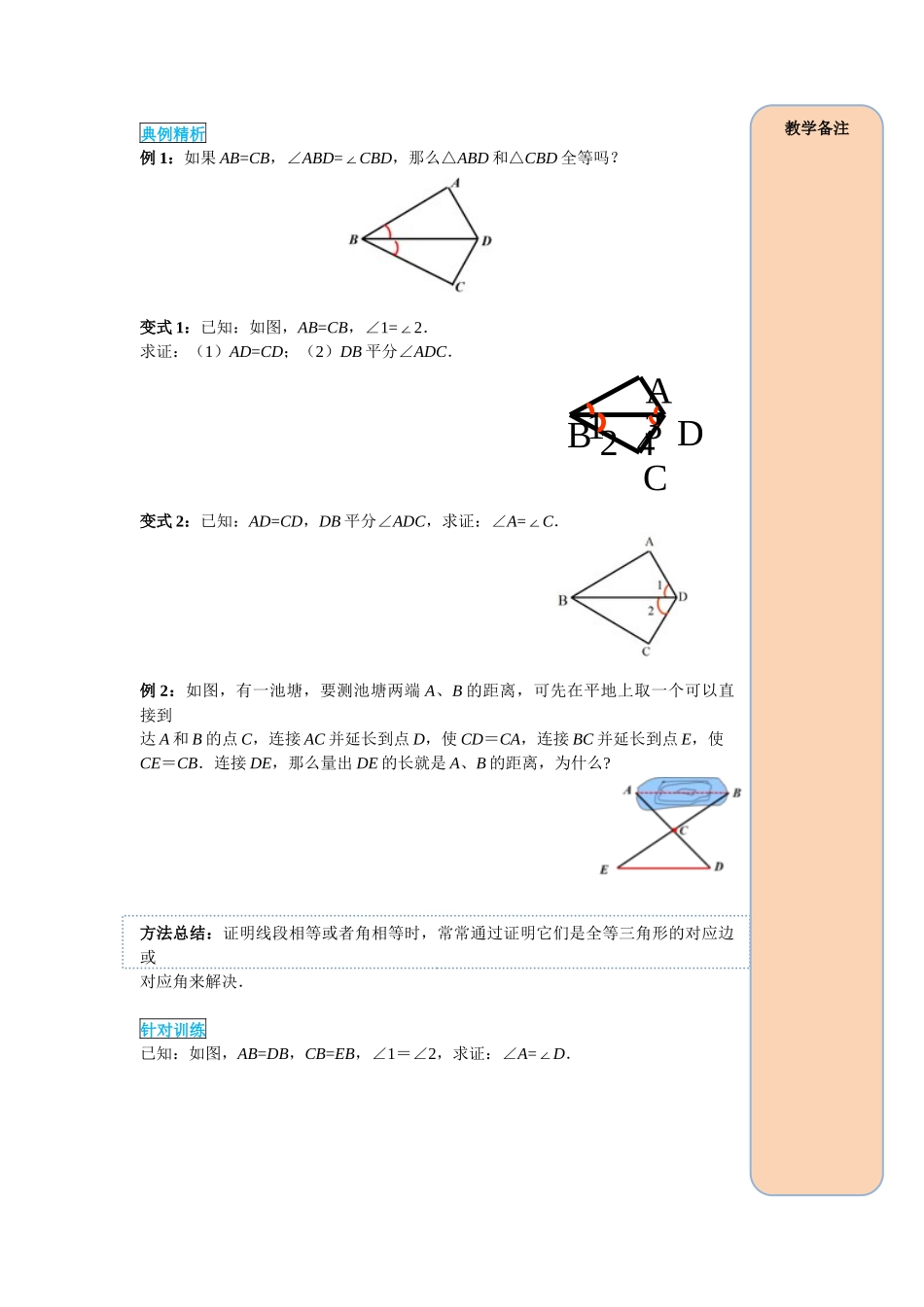
第十二章 全等三角形12.2 全等三角形的判定第 2 课时 “边角边”学习目标:1.掌握三角形全等的“边角边”的条件. 2.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程. 3.能运用“SAS”证明简单的三角形全等问题.重点:掌握一般三角形全等的判定方法 SAS.难点:运用全等三角形的判定方法解决证明线段或角相等的问题.一、要点探究探究点 1:三角形全等的判定(“边角边”)问题:已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置上有几种可能性呢?探究活动 1:SAS 能否判定两个三角形全等动手试一试:尺规作图画出一个△A′B′C′,使 A′B′=AB,A′C′=AC,∠A′=∠A(即使两边和它们的夹角对应相等).把画好的△A′B′C′剪下,放到△ABC 上,它们全等吗?知识要点: “边角边”判定方法文字语言:两边和它们的夹角分别相等的两个三角形全等(简写成“边角边”或“SAS”).几何语言:在△ABC 和△DEF 中,∴△ABC≌△DEF(SAS). 课堂探究教学备注配套 PPT 讲授1.情景引入(见幻灯片 3-4)2.探究点 1 新知讲授( 见 幻 灯 片 5-13)典例精析例 1:如果 AB=CB,∠ABD=∠CBD,那么△ABD 和△CBD 全等吗? 变式 1:已知:如图,AB=CB,∠1=2∠ . 求证:(1)AD=CD;(2)DB 平分∠ADC.变式 2:已知:AD=CD,DB 平分∠ADC,求证:∠A=∠C.例 2:如图,有一池塘,要测池塘两端 A、B 的距离,可先在平地上取一个可以直接到达 A 和 B 的点 C,连接 AC 并延长到点 D,使 CD=CA,连接 BC 并延长到点 E,使CE=CB.连接 DE,那么量出 DE 的长就是 A、B 的距离,为什么?方法总结:证明线段相等或者角相等时,常常通过证明它们是全等三角形的对应边或对应角来解决.针对训练已知:如图,AB=DB,CB=EB,∠1=∠2,求证:∠A=∠D. ADBC12 43教学备注探究活动 2:“SSA”不能作为判定三角形全等的依据想一想:如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住长木棍,转动短木棍,得到△ABD.这个实验说明了什么? 画一画:画△ABC 和△ABD,使∠A=∠A=30°,AB=AB=5 cm,BC=BD=3 cm.观察所得的两个三角形是否全等?要点归纳:有两边和其中一边的对角分别相等的两个三角形______全等.典例精析例 3:下列条件中,不能证明△ABC≌△DEF 的是( )A.AB=DE,∠B=∠E,BC=EFB.AB=DE,∠A=∠D,AC=DFC.BC=EF,...