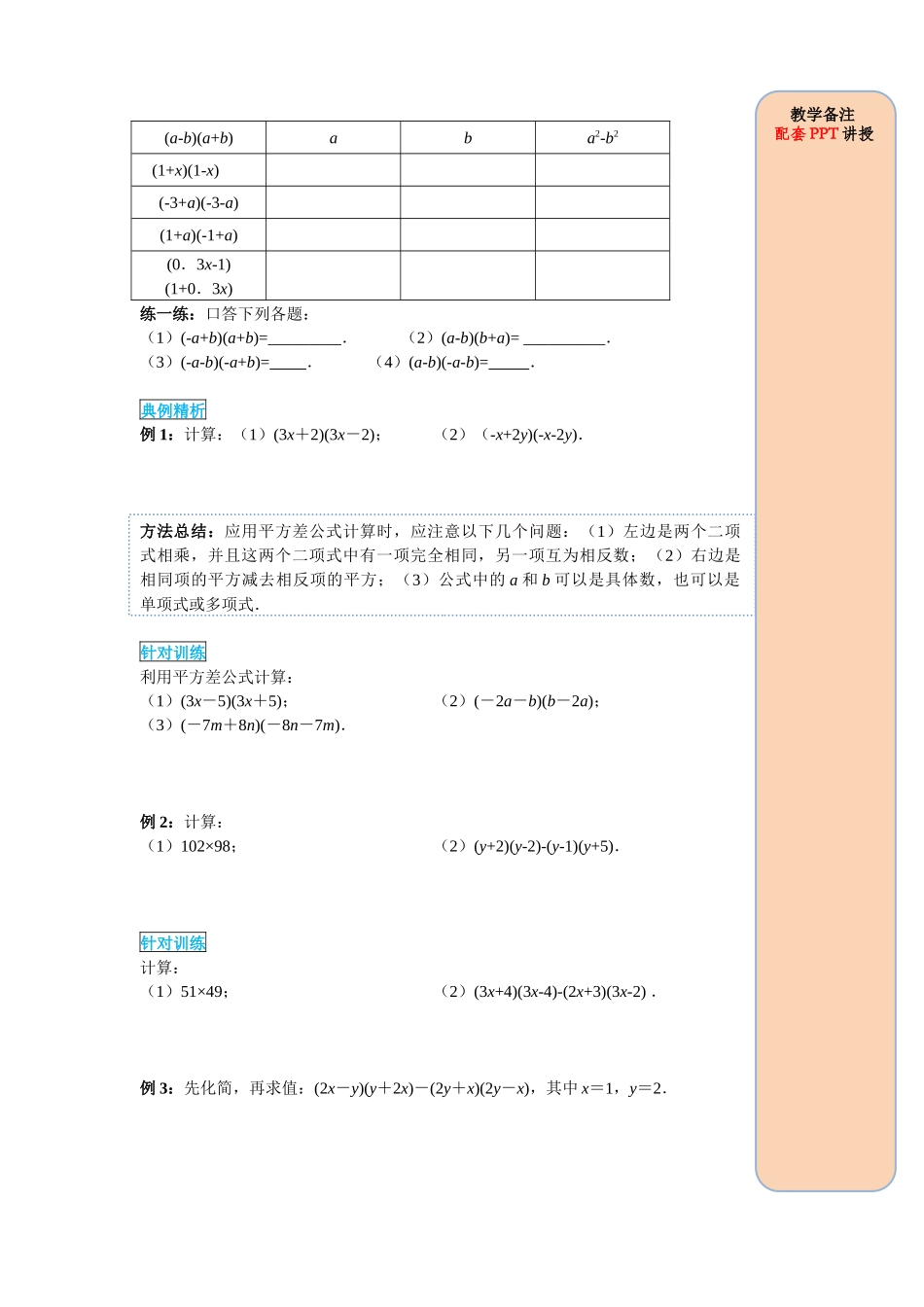
第十四章 整式的乘法与因式分解 14.2 乘法公式 14.2.1 平方差公式学习目标:1.经历平方差公式的探索及推导过程,掌握平方差公式的结构特征.2.灵活应用平方差公式进行计算和解决实际问题.重点:掌握平方差公式的结构特征.难点:应用平方差公式进行计算和解决实际问题.一、知识链接1.多项式乘多项式的乘法法则:多项式与多项式相乘,先用一个多项式的每一项_________另一个多项式的每一项,再把所得的积_______.2.计算:(1)(x+1)(x+3)=_________________;(2)(x+3)(x-3)=________________;(3)(m+n)(m-n)=________________.一、要点探究探究点:平方差公式算一算:计算下列多项式的积,你能发现什么规律?①(x+1)(x-1)=_______________;②(m+2)(m-2)=_______________; ③(2m+1)(2m-1)=_______________; ④(5y+z)(5y-z)=_______________.想一想:这些计算结果有什么特点?要点归纳:平方差公式:(a+b)(a−b)=_________,即两数和与这两数差的积,等于这两数的__________.公式变形:1.(a-b)(a+b)= a2-b22.(b+a)(-b+a)= a2-b2填一填:自主学习课堂探究教学备注学 生 在 课 前完 成 自 主 学习部分1.复习引入( 见 幻 灯 片3)2.探究点新知讲授( 见 幻 灯 片4-19)(a-b)(a+b)aba2-b2 (1+x)(1-x)(-3+a)(-3-a)(1+a)(-1+a)(0.3x-1)(1+0.3x)练一练:口答下列各题:(1)(-a+b)(a+b)=_________.(2)(a-b)(b+a)= __________.(3)(-a-b)(-a+b)= .(4)(a-b)(-a-b)= .典例精析例 1:计算:(1)(3x+2)(3x-2);(2)(-x+2y)(-x-2y).方法总结:应用平方差公式计算时,应注意以下几个问题:(1)左边是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;(2)右边是相同项的平方减去相反项的平方;(3)公式中的 a 和 b 可以是具体数,也可以是单项式或多项式.针对训练利用平方差公式计算:(1)(3x-5)(3x+5);(2)(-2a-b)(b-2a);(3)(-7m+8n)(-8n-7m).例 2:计算:(1)102×98;(2)(y+2)(y-2)-(y-1)(y+5).针对训练计算:(1)51×49;(2)(3x+4)(3x-4)-(2x+3)(3x-2) .例 3:先化简,再求值:(2x-y)(y+2x)-(2y+x)(2y-x),其中 x=1,y=2.教学备注配套 PPT 讲授例 4:对于任意的正整数 n,整式(3n+1)(3n-1)-(3-n)(3+n)的值一定是 10 的整数倍吗?方法总结:对于平方差中的 a 和 b 可以是具体的数,...