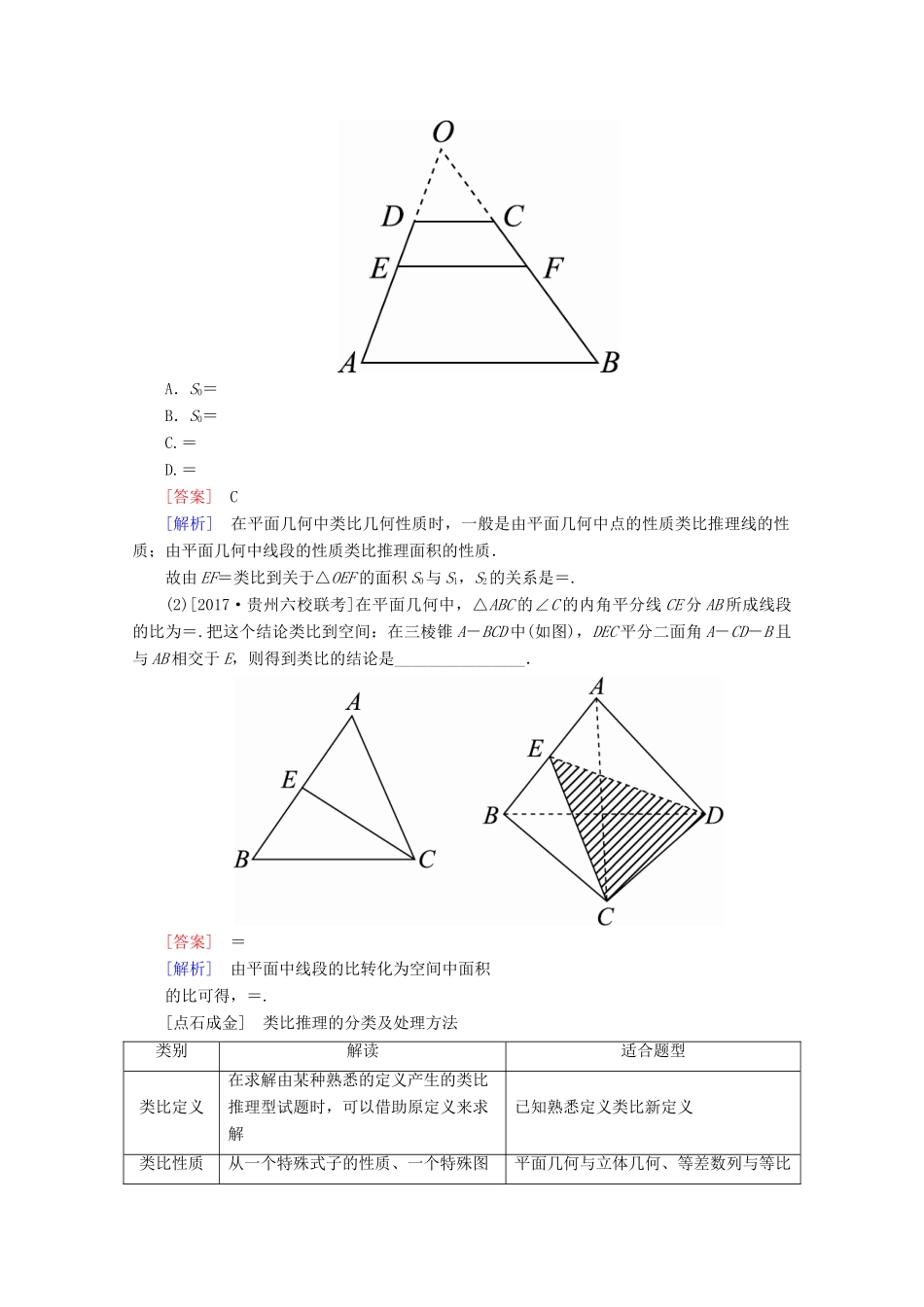
§12.1 合情推理与演绎推理考纲展示► 1.了解合情推理的含义,能利用归纳和类比等进行简单的推理,了解合情推理在数学发展中的作用.2.了解演绎推理的重要性,掌握演绎推理的基本模式,并能运用它们进行一些简单推理.3.了解合情推理和演绎推理之间的联系和差异.考点 1 类比推理 类比推理(1)① 定义:由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有________的推理.(2)特点:是由________到________的推理.答案:(1)这些特征 (2)特殊 特殊[教材习题改编]在 Rt△ABC 中,两直角边分别为 a,b,设 h 为斜边上的高,则=+.由此类比:三棱锥 S-ABC 中的三条侧棱 SA,SB,SC 两两垂直,且长度分别为 a,b,c,设棱锥底面 ABC 上的高为 h,则________.答案:=++解析:直角三角形的两直角边对应该三棱锥的三条两两垂直的侧棱,直角三角形斜边上的高对应该三棱锥底面上的高,类比得=++.事实上,在直角三角形中=+是由等面积法得到的,而在三棱锥中可由等体积法求得=++[典题 1] (1)[2017·江西南昌模拟]如图,在梯形 ABCD 中,AB∥CD,AB=a,CD=b(a>b).若 EF∥AB,EF 到 CD 与 AB 的距离之比为 m∶n,则可推算出:EF=.用类比的方法,推想出下面问题的结果.在上面的梯形 ABCD 中,分别延长梯形的两腰 AD 和 BC 交于 O 点,设△OAB,△ODC 的面积分别为 S1,S2,则△OEF 的面积 S0与 S1,S2的关系是( )A.S0= B.S0=C.= D.=[答案] C[解析] 在平面几何中类比几何性质时,一般是由平面几何中点的性质类比推理线的性质;由平面几何中线段的性质类比推理面积的性质.故由 EF=类比到关于△OEF 的面积 S0与 S1,S2的关系是=.(2)[2017·贵州六校联考]在平面几何中,△ABC 的∠C 的内角平分线 CE 分 AB 所成线段的比为=.把这个结论类比到空间:在三棱锥 A-BCD 中(如图),DEC 平分二面角 A-CD-B 且与 AB 相交于 E,则得到类比的结论是________________.[答案] =[解析] 由平面中线段的比转化为空间中面积的比可得,=.[点石成金] 类比推理的分类及处理方法类别解读适合题型类比定义在求解由某种熟悉的定义产生的类比推理型试题时,可以借助原定义来求解已知熟悉定义类比新定义类比性质从一个特殊式子的性质、一个特殊图平面几何与立体几何、等差数列与等比形的性质入手,提出类比推理型问题,求解时要认真分析两者之间的联...