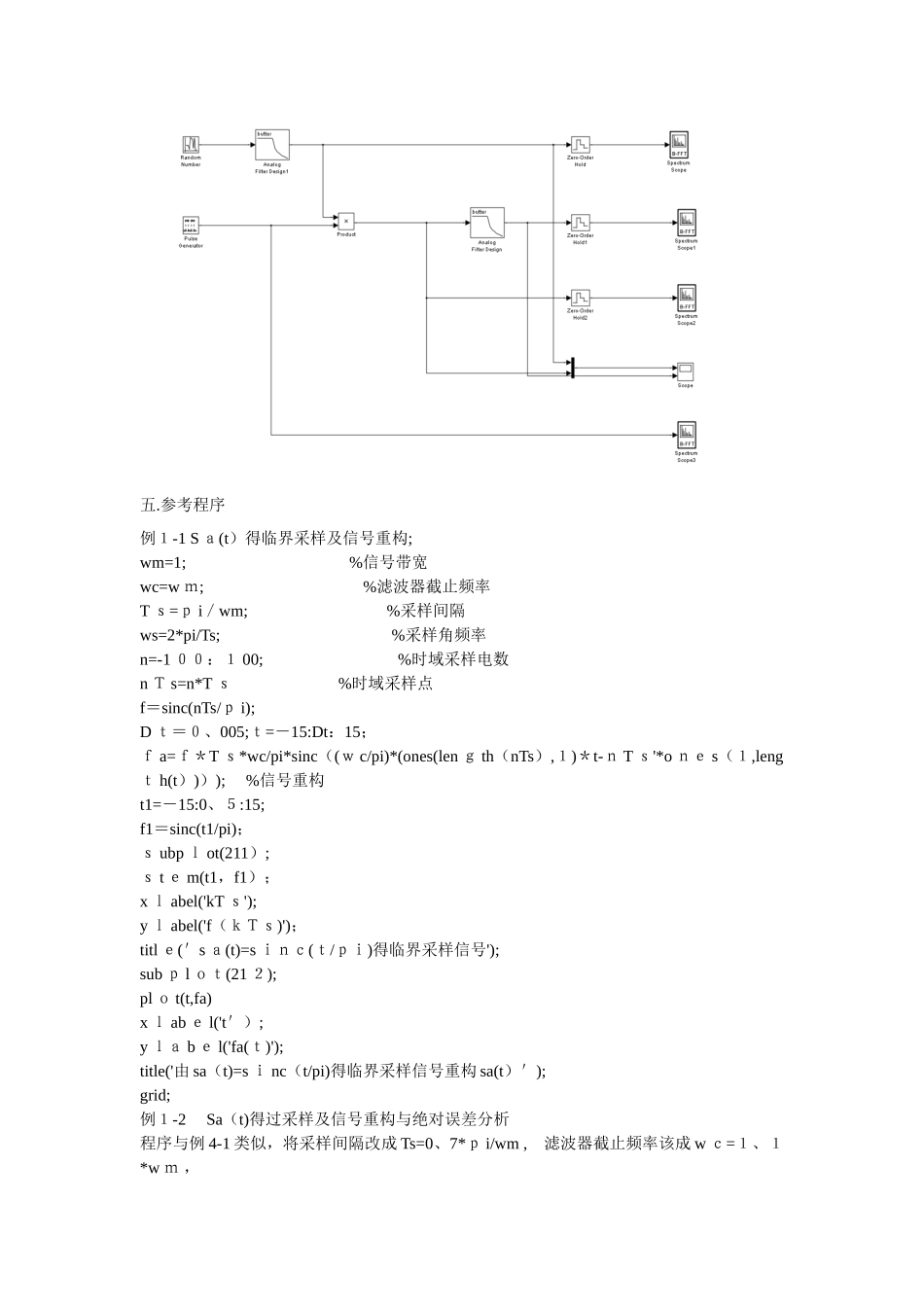
实验一 信号抽样与恢复一、实验目得学会用 MATLAB 实现连续信号得采样与重建二、实验原理 1.抽样定理若就是带限信号,带宽为, 经采样后得频谱就就是将得频谱 在频率轴上以采样频率为间隔进行周期延拓。因此,当时,不会发生频率混叠;而当 < 时将发生频率混叠。2.信号重建经采样后得到信号经理想低通则可得到重建信号,即:=*其中:==所以:=*=* =上式表明,连续信号可以展开成抽样函数得无穷级数。利用 MATLA B中得来表示,有 ,所以可以得到在M ATLAB 中信号由重建得表达式如下:=我们选取信号=作为被采样信号,当采样频率=2 时,称为临界采样。我们取理想低通得截止频率=。下面程序实现对信号=得采样及由该采样信号恢复重建:三、上机实验内容1.验证实验原理中所述得相关程序;2.设 f(t)=0、5*(1+c o st)*(u(t+p i)-u(t-pi)) ,由于不就是严格得频带有限信号,但其频谱大部分集中在[0,2]之间,带宽 wm 可根据一定得精度要求做一些近似。试根据以下两种情况用 M A TL A B 实现由f(t)得抽样信号f s(t)重建 f(t) 并求两者误差,分析两种情况下得结果。(1) wm=2 , wc=1、2 w m , T s=1;(2) w m=2 , wc=2 , T s=2、53.对以下 s i mul i nk ch 6 ex a mpl e1_H e 7、mdl 低通采样定理以程序实现,具体参数参考框图内参数。五.参考程序例1-1 S a(t)得临界采样及信号重构;wm=1; %信号带宽wc=w m; %滤波器截止频率T s=p i/wm; %采样间隔ws=2*pi/Ts; %采样角频率 n=-1 00:1 00; %时域采样电数n T s=n*T s %时域采样点f=sinc(nTs/p i);D t=0、005;t=-15:Dt:15;f a=f*T s*wc/pi*sinc((w c/pi)*(ones(len g th(nTs),1)*t-n T s'*o ne s(1,lengt h(t)))); %信号重构t1=-15:0、5:15;f1=sinc(t1/pi);s ubp l ot(211);s t e m(t1,f1);x l abel('kT s');y l abel('f(kTs)');titl e('s a(t)=s inc(t/pi)得临界采样信号');sub p l ot(21 2);pl o t(t,fa)x l ab e l('t');y la b e l('fa(t)');title('由 sa(t)=s i nc(t/pi)得临界采样信号重构 sa(t)');grid;例1-2 Sa(t)得过采样及信号重构与绝对误差分析程序与例 4-1 类似,将采样间隔改成 Ts=0、7*p i/wm , 滤波器截止频率该成 w c=1、1*w m ,添加一...