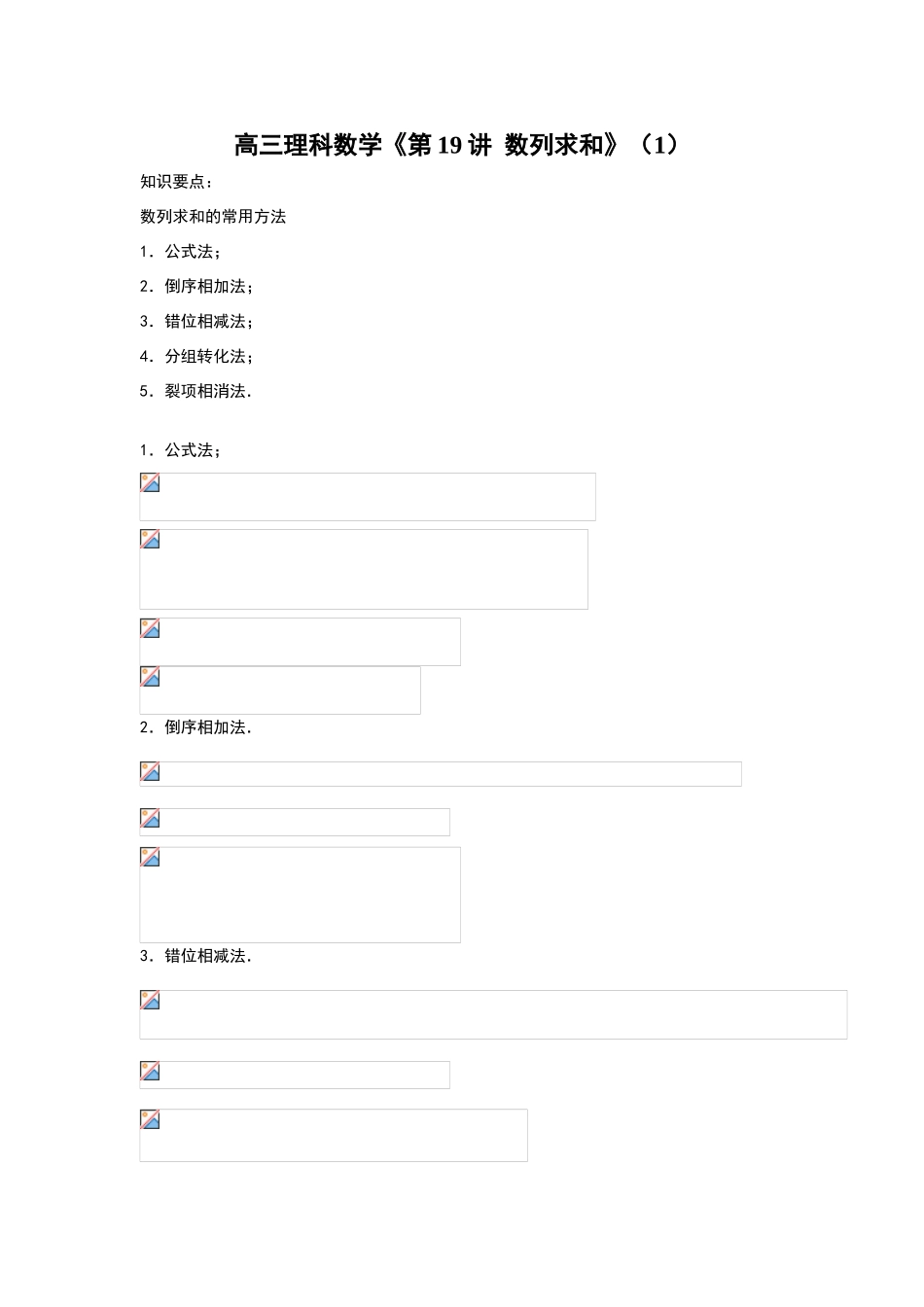
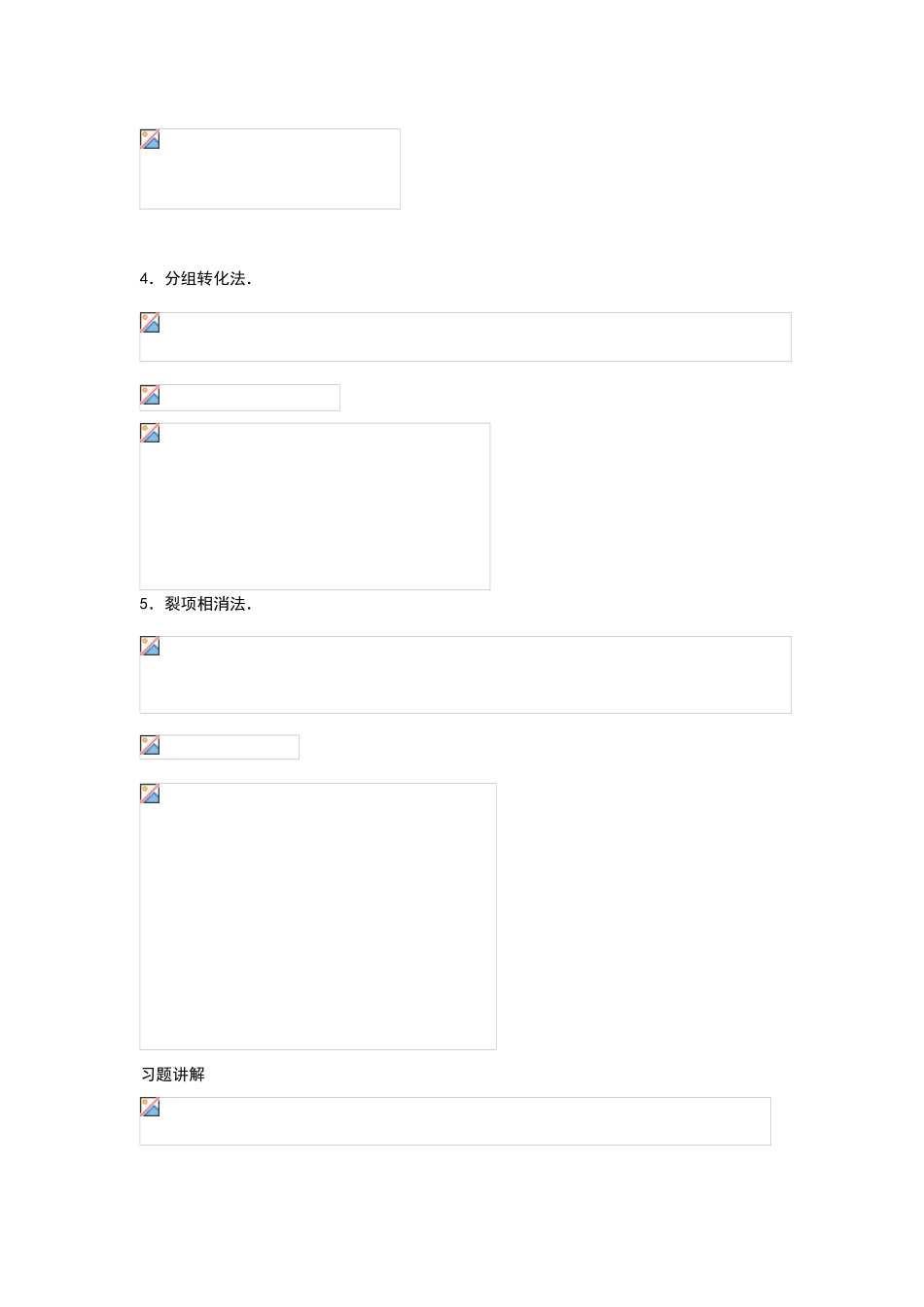
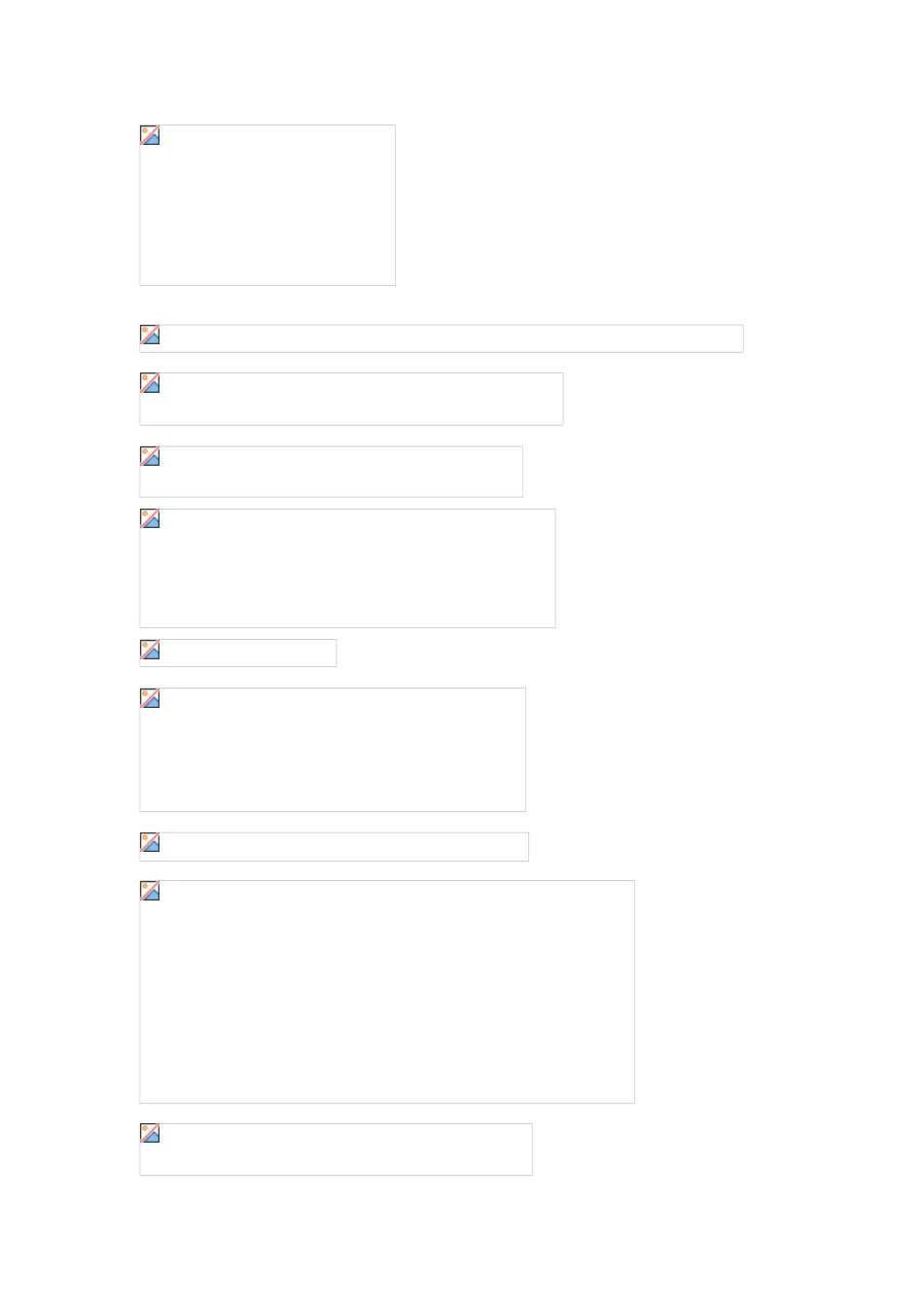
高三理科数学《第 19 讲 数列求和》(1)知识要点:数列求和的常用方法1.公式法;2.倒序相加法;3.错位相减法;4.分组转化法;5.裂项相消法.1.公式法;2.倒序相加法.3.错位相减法.4.分组转化法.5.裂项相消法.习题讲解 练习求下列各项的和(1)Sn=1+(3+4)+(5+6+7)+…+(2n – 1+2n+…+3n –2)(2)Sn=12–22+32– 42+…+(– 1n–1·n2【解析】(1)∵an=(2n–1)+2n+(2n+1)+…+[(2n – 1)+ n – 1] =,∴Sn=…+n2)–(1+2+…+n)=.(2)当 n 是偶数时, [(n–1)2–n2]= –3–7…–(2n+1) =.当 n 是奇数时,Sn=1+(32–22)+(52– 42)+…+ [n2– (n–1)] =1 + 5 + 9 +…+(2n–1)=.故 Sn=.小结高三理科数学《第 19 讲 数列求和》(2)例 1 已知数列{an}满足 a1 = 1,(n∈N *,n>1). (1)求证:数列{}是等差数列;(2)求数列{ anan + 2}的前 n 项和 Sn;(3)设(a∈R),求数列{bn}的前 n 项和 Tn.【解析】(1)当 n≥2 时,由得:an – 1 – an – 2 an – 1 an = 0,两边同除 an an – 1,得∴{}是以为首项,d = 2 为公差的等差数列.(2)由(1)知,= 1 + ( n – 1 )×2 = 2n – 1,∴an =∴an an +2 =,…+(3)∵bn =∴,当 a = 0 时,Tn = 0;当 a = 1 时,Tn = n2;当 a≠0 且 a≠1 时,由于 Tn = a + 3a2 + 5a3 +…+(2n – 1)an ①∴aTn = a2 + 3a3 + 5a4+…+(2n – 1)an + 1 ②① – ② 得:(1 – a)Tn = a + 2(a2 + a3 +…+an) – (2n – 1)an + 1,∴,故例 2 如果有穷数列 a1,a2,…,am(m 为正整数)满足条件 a1 = am,a2 = am – 1 …,am = a1,即ai = am – i + 1 (i = 1,2,…,m ),我们称其为“对称数列”.例如,数列 1,2,5,2,1 与数列 8,4,2,2,4,8 都是“对称数列”.(1)设{bn}是 7 项的“对称数列”,其中 b1,b2,b3,b4是等差数列,且 b1 = 2,b4 = 11,依次写出{bn}的每一项;(2)设{cn}是 49 项的“对称数列”,其中 c25,c26,…,c49是首项为 1,公比为 2 的等比数列,求{cn}的各项的和 S;(3)设{dn}是 100 项的“对称数列”,其中 d51,d52,…,d100是首项为 2,公差为 3的等差数列,求{dn}前 n 项的和 Sn(n = 1,2,…100).【解析】(1)设数列{bn}前四项的差为 d,则 b4 = b1 + 3d = 2 + 3d = 11,解得 d = 3,∴数列{bn}为 2,5,8,11,8,5,2.(2)S = c1 + c2+…+c49 = 2(c25 + c26 +…+ c49) – c25 = 2 (1 + 2 + 22 + …224) – 1 = 2 (225 – 1) – 1 = 226 – 3 = 67108861.(3)d51 = 2,d100 = 2 + 3×(50 – 1) = 149.由题意得 d1,d2,…,d50是首项为 149,公差为 – 3 的等差数列,当 n≤50 时,Sn = d1 + d2 + … + dn.= 149n +当 51≤n≤100 时,Sn = d1 + d2 + … + dn= S50 + (d51 + d52 + … + dn)= 3775 + 2×(n – 50) + =综上所述,Sn =