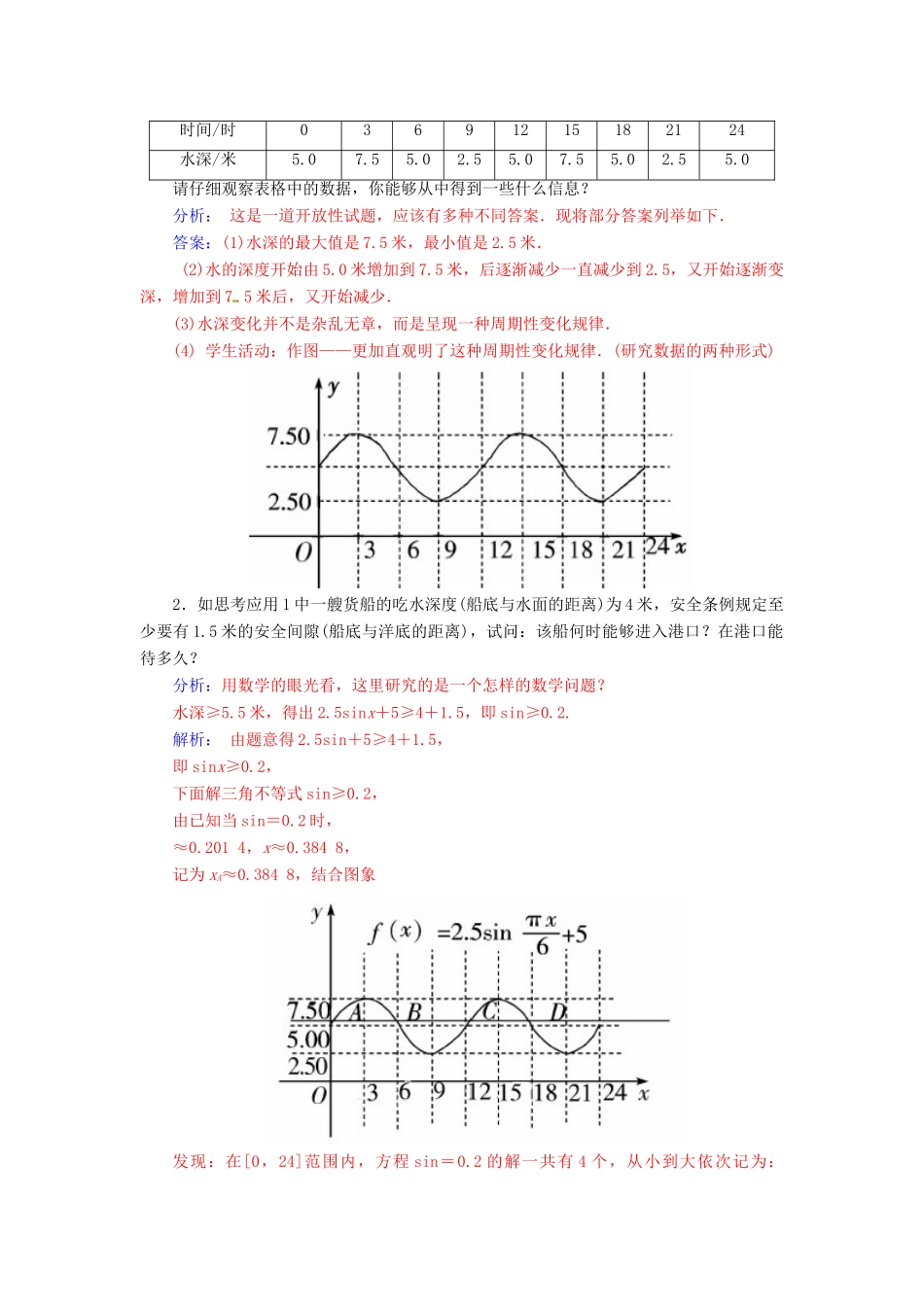
第一章 三角函数三角函数1.6 三角函数模型的简单应用1.了解曲线 y=Asin(ωx+φ)在物理上的应用,了解建立该类问题的数学模型所应掌握的物理知识.2.理解并掌握解数学应用问题的一般步骤,掌握将所发现的规律抽象为恰当的三角函数问题的方法,并能正确选择恰当的角作为变量建立函数关系.三角函数模型的简单应用1.建立三角函数模型解决实际问题.三角函数在数学中有着广泛的应用,在实际生活中也可以解决很多问题,如某天某段时间内温度的变化规律等.如果某种现象的变化具有周期性,根据三角函数的性质,我们可以根据这一现象的特征和条件,利用三角函数知识构建数学模型,从而把这一具体现象转化为一个特定的数学模型——三角函数模型.2.解三角函数应用题的基本步骤.第一步,阅读理解,审清题意.读题要做 到逐字逐句,读懂题中的文字叙述,理解叙述所反映的实际背景,在此基础上,分析出已知什么,求什么,从中提炼出相应的数学问题.第二步,搜集整理数据,建立数学模型.根据搜集到的数据,找出变化规律,运用已掌握的三角知识、物理知识以及其他相关知识建立关系式,在此基础上将实际问题转化为一个三角函数问题,实现问题的数学化,即建立三角函数模型.第三步,利用所学的三角知识对得到的三角函数模型予以解答,求得结果.第四步,将所得结论转译成实际问题的答案.1.下面是钱塘江某个码头今年春季每天的时间(单位:时)与水深(单位:米)的关系表:时间/时03691215182124水深/米5.07.55.02.55.07.55.02.55.0请仔细观察表格中的数据,你能够从中得到一些什么信息?分析: 这是一道开放性试题,应该有多种不同答案.现将部分答案列举如下.答案:(1)水深的最大值是 7.5 米,最小值是 2.5 米. (2)水的深度开始由 5.0 米增加到 7.5 米,后逐渐减少一直减少到 2.5,又开始逐渐变深,增加到 7 .5 米后,又开始减少.(3)水深变化并不是杂乱无章,而是呈现一种周期性变化规律.(4) 学生活动:作图——更加直观明了这种周期性变化规律.(研究数据的两种形式)2.如思考应用 1 中一艘货船的吃水深度(船底与水面的距离)为 4 米,安全条例规定至少要有 1.5 米的安全间隙(船底与洋底的距离),试问:该船何时能够进入港口?在港口能待多久?分析:用数学的眼光看,这里研究的是一个怎样的数学问题?水深≥5.5 米,得出 2.5sinx+5≥4+1.5,即 sin≥0.2.解析: 由题意得 2.5sin+5≥4+1.5,即 sinx≥0.2,下面...