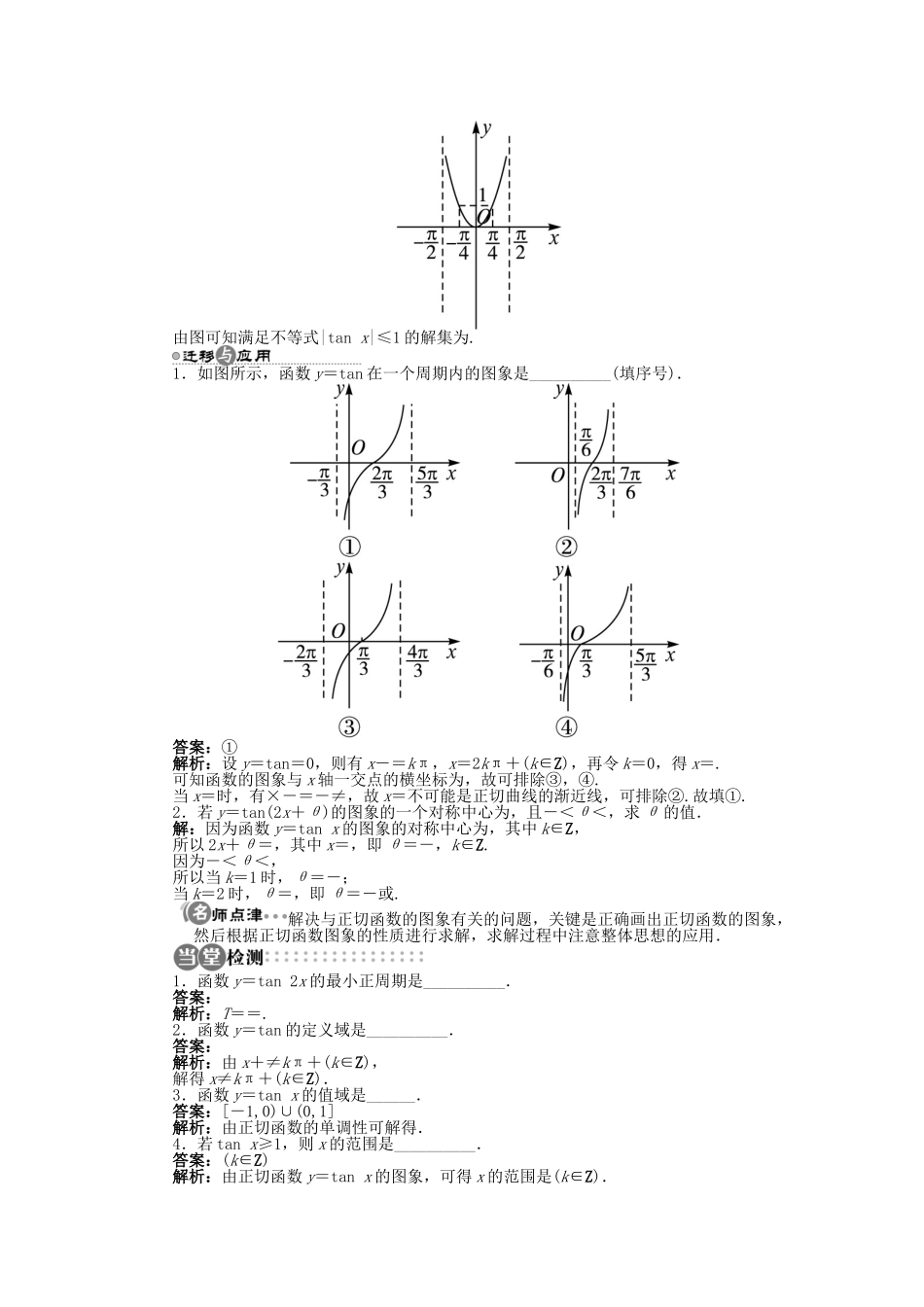
1.3.2 三角函数的图象和性质第 2 课时 正切函数的图象和性质学习目标重点难点1.能画出正切函数的图象.2.理解正切函数在上的性质.3.会利用正切函数的性质解决一些简单问题.重点:正切函数的图象与性质.难点:理解正切函数在上的性质,并会运用性质解决简单问题.正切函数的图象与性质正切函数的图象叫做正切曲线.正切函数的性质如下表:定义域值域R周期性周期函数,T=π奇偶性奇函数,图象关于原点对称单调性在(k∈Z)上是增函数对称性中心对称图形,对称中心为(k∈Z)预习交流 1正切函数在整个定义域内是增函数吗?提示:不是.正切曲线由被互相平行的直线 x=+kπ(k∈Z)所隔开的无穷多支曲线组成,且不连续.例如取 x1=,x2=,显然 x1<x2,但 y1=tan=1,y2=tan=-,∴y1>y2,不符合增函数定义.预习交流 2如何作出正切函数的图象?提示:(1)几何法利用单位圆中的正切线来作出正切函数的图象,该方法作图较为精确,但画图时较繁琐.(2)三点两线法“三点”是指,(0,0),;“两线”是指 x=-和 x=.在三点、两线确定的情况下,类似于五点法作图,可大致画出正切函数在上的简图,然后向右、向左扩展即可得到正切曲线.一、正切函数的定义域、值域问题求函数 y=+lg(1-tan x)的定义域.思路分析:先列出使每个式子有意义的不等式组,然后解不等式组.解:由题意得即-1≤tan x<1.在内,满足上述不等式的 x 的取值范围是.又因为 y=tan x 的周期为 π,所以所求 x 的范围是(k∈Z).故函数的定义域为(k∈Z).求函数 y=的定义域.解:要使 y=有意义,必须满足即∴函数 y=的定义域为∪(k∈Z).求正切函数的定义域、值域的方法及注意点:(1)求与正切函数有关的函数的定义域时,除了求函数定义域的一般要求外,还要保证正切函数 y=tan x 有意义,即 x≠kπ+(k∈Z),而对于构建的三角函数不等式,常利用三角函数的图象求解.(2)求解与正切函数有关的函数的值域时,要注意函数的定义域,在定义域内求值域;对于求由正切函数复合而成的函数的值域时,常利用换元法,但要注意新“元”的范围.二、与正切函数有关的函数的单调性问题求函数 y=tan 的单调减区间.思路分析:将函数化为 y=-tan,再利用整体代换求解.解: y=tan=-tan,∴只需求函数 y=tan 的单调增区间,即为原函数的单调减区间.令 μ=-,则 μ∈(k∈Z),即-+kπ<μ<+kπ(k∈Z).∴-+kπ<-<+kπ(k∈Z).解得 4k...