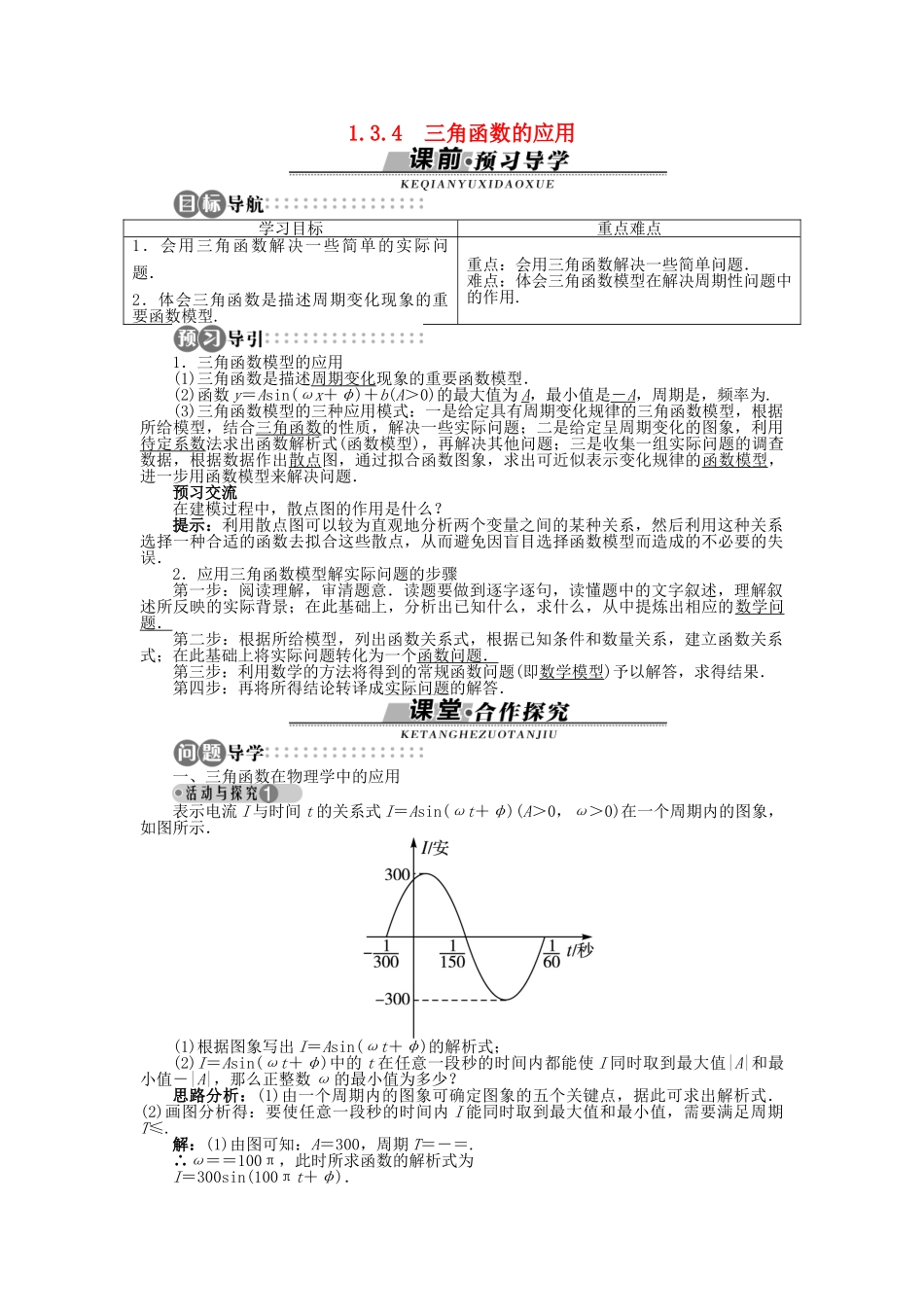
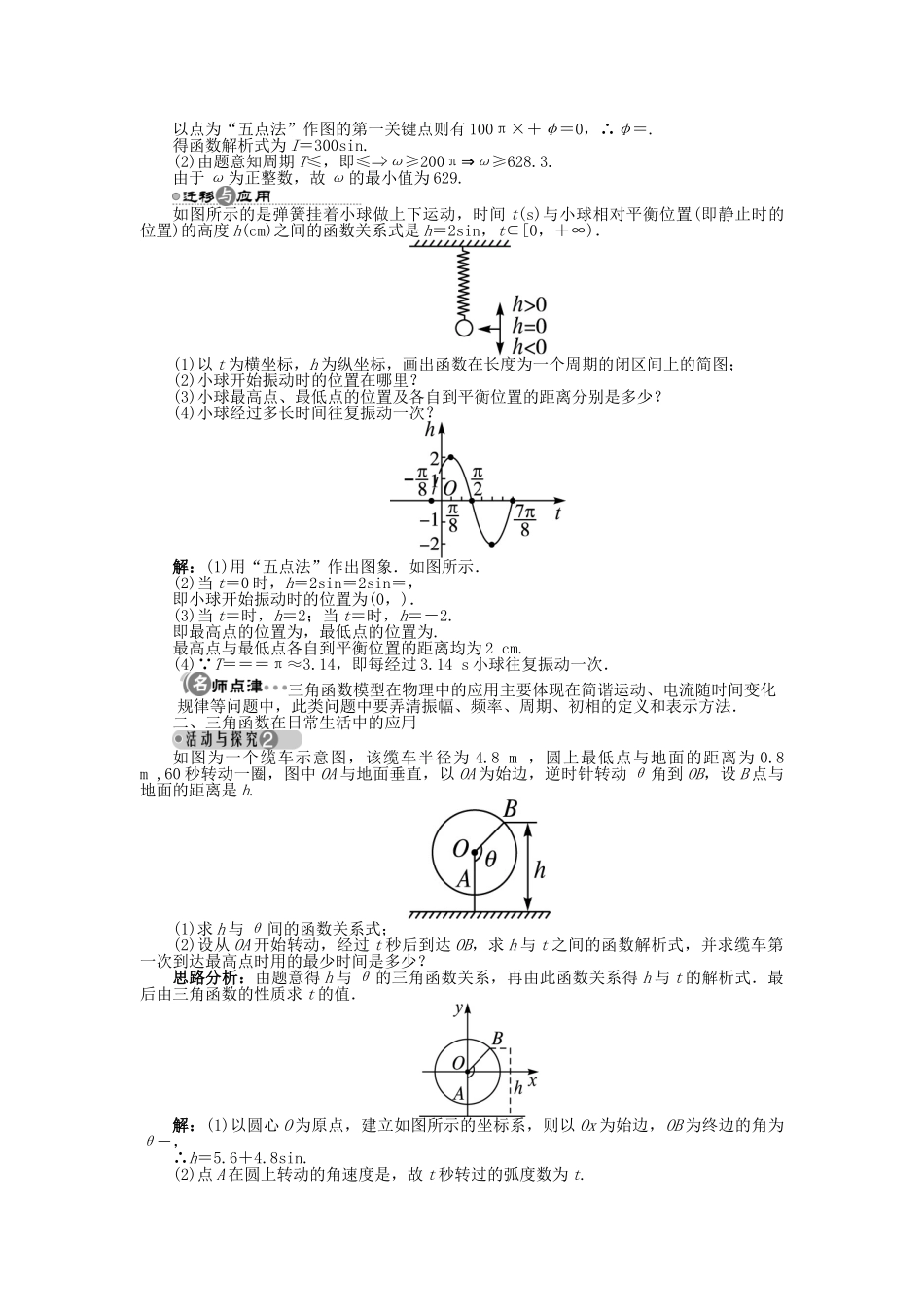
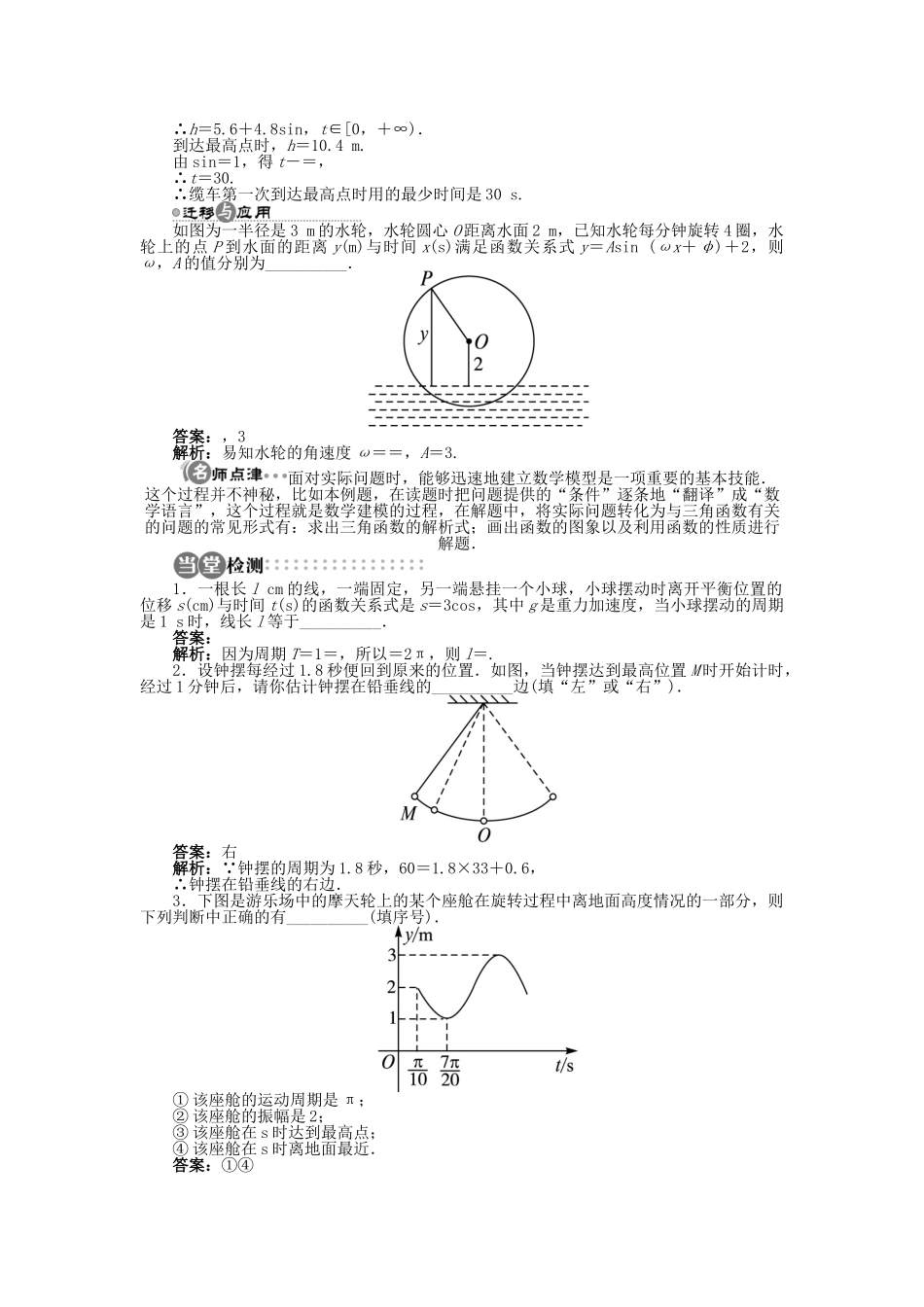
1.3.4 三角函数的应用学习目标重点难点1.会用三角函数解决一些简单的实际问题.2.体会三角函数是描述周期变化现象的重要函数模型.重点:会用三角函数解决一些简单问题.难点:体会三角函数模型在解决周期性问题中的作用.1.三角函数模型的应用(1)三角函数是描述周期变化现象的重要函数模型.(2)函数 y=Asin(ωx+φ)+b(A>0)的最大值为 A,最小值是- A ,周期是,频率为.(3)三角函数模型的三种应用模式:一是给定具有周期变化规律的三角函数模型,根据所给模型,结合三角函数的性质,解决一些实际问题;二是给定呈周期变化的图象,利用待定系数法求出函数解析式(函数模型),再解决其他问题;三是收集一组实际问题的调查数据,根据数据作出散点图,通过拟合函数图象,求出可近似表示变化规律的函数模型,进一步用函数模型来解决问题.预习交流在建模过程中,散点图的作用是什么?提示:利用散点图可以较为直观地分析两个变量之间的某种关系,然后利用这种关系选择一种合适的函数去拟合这些散点,从而避免因盲目选择函数模型而造成的不必要的失误.2.应用三角函数模型解实际问题的步骤第一步:阅读理解,审清题意.读题要做到逐字逐句,读懂题中的文字叙述,理解叙述所反映的实际背景;在此基础上,分析出已知什么,求什么,从中提炼出相应的数学问题.第二步:根据所给模型,列出函数关系式,根据已知条件和数量关系,建立函数关系式;在此基础上将实际问题转化为一个函数问题.第三步:利用数学的方法将得到的常规函数问题(即数学模型)予以解答,求得结果.第四步:再将所得结论转译成实际问题的解答.一、三角函数在物理学中的应用表示电流 I 与时间 t 的关系式 I=Asin(ωt+φ)(A>0,ω>0)在一个周期内的图象,如图所示.(1)根据图象写出 I=Asin(ωt+φ)的解析式;(2)I=Asin(ωt+φ)中的 t 在任意一段秒的时间内都能使 I 同时取到最大值|A|和最小值-|A|,那么正整数 ω 的最小值为多少?思路分析:(1)由一个周期内的图象可确定图象的五个关键点,据此可求出解析式.(2)画图分析得:要使任意一段秒的时间内 I 能同时取到最大值和最小值,需要满足周期T≤.解:(1)由图可知:A=300,周期 T=-=.∴ω==100π,此时所求函数的解析式为I=300sin(100πt+φ).以点为“五点法”作图的第一关键点则有 100π×+φ=0,∴φ=.得函数解析式为 I=300sin.(2)由题意知周期 T≤,即≤⇒ω≥200π⇒ω≥628.3.由于...