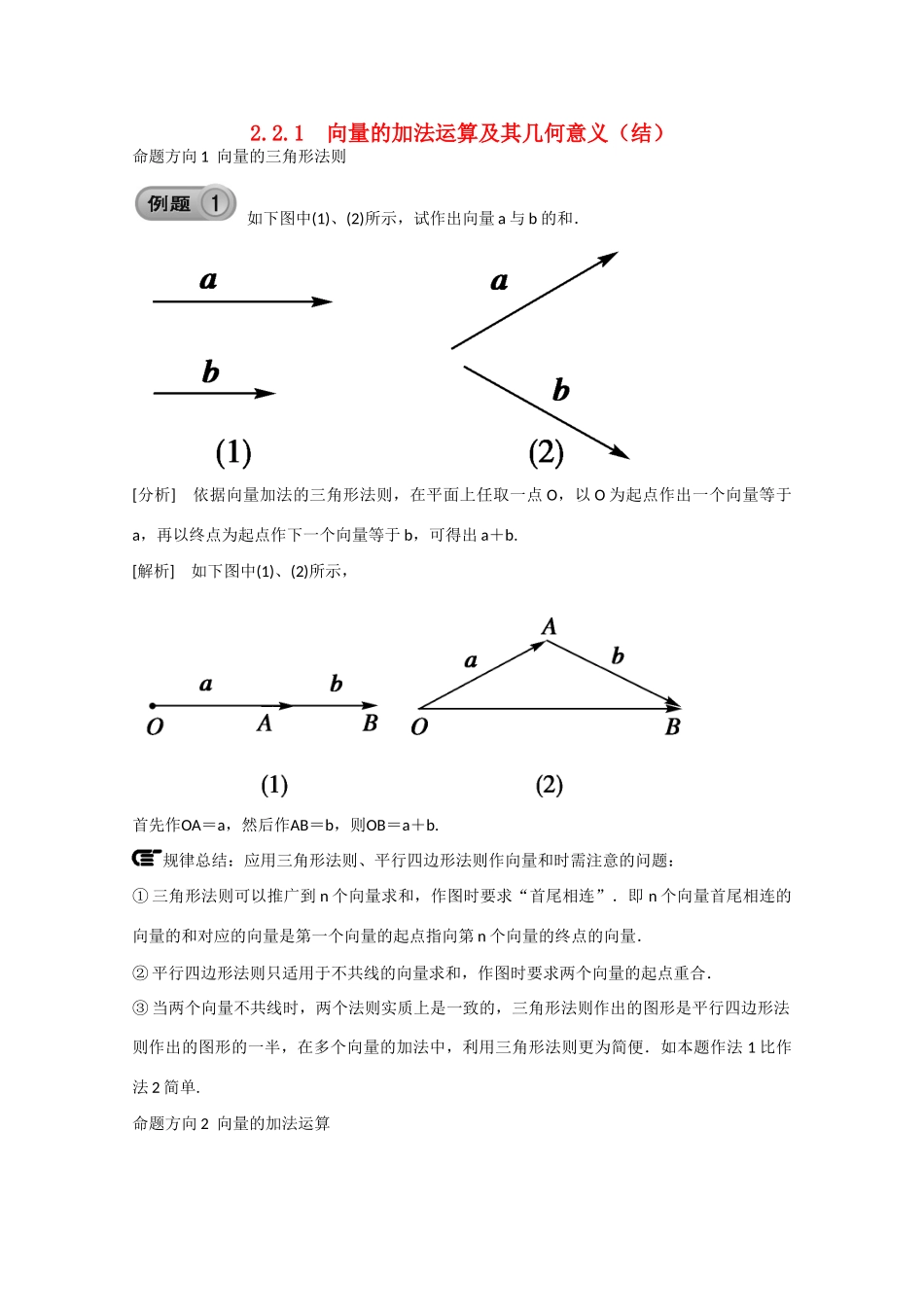
2.2.1 向量的加法运算及其几何意义(结)命题方向 1 向量的三角形法则 如下图中(1)、(2)所示,试作出向量 a 与 b 的和.[分析] 依据向量加法的三角形法则,在平面上任取一点 O,以 O 为起点作出一个向量等于a,再以终点为起点作下一个向量等于 b,可得出 a+b.[解析] 如下图中(1)、(2)所示,首先作OA=a,然后作AB=b,则OB=a+b.规律总结:应用三角形法则、平行四边形法则作向量和时需注意的问题:① 三角形法则可以推广到 n 个向量求和,作图时要求“首尾相连”.即 n 个向量首尾相连的向量的和对应的向量是第一个向量的起点指向第 n 个向量的终点的向量.② 平行四边形法则只适用于不共线的向量求和,作图时要求两个向量的起点重合.③ 当两个向量不共线时,两个法则实质上是一致的,三角形法则作出的图形是平行四边形法则作出的图形的一半,在多个向量的加法中,利用三角形法则更为简便.如本题作法 1 比作法 2 简单.命题方向 2 向量的加法运算 化简下列各式:(1)AB+BC+CD+DA;(2)(AB+MB)+BO+OM.[解析] (1)AB+BC+CD+DA=(AB+BC)+(CD+DA)=AC+CA=0;(2)(AB+MB)+BO+OM=(AB+BO)+(OM+MB)=AO+OB=AB.命题方向 3 向量加法的实际应用 如图,在重 300 N 的物体上拴两根绳子,这两根绳子在铅垂线的两侧,与铅垂线的夹角分别为 30°、60°,求当整个系统处于平衡状态时,两根绳子拉力的大小.[解析] 如图,作▱OACB,使∠AOC=30°,∠BOC=60°,OA和OB分别表示两根绳子的拉力,则OC表示这两根绳子拉力的合力,则|OC|=300 N.在△OAC 中,∠ACO=∠BOC=60°,∠OAC=90°.则|OA|=|OC|cos30°=300×=150(N),|AC|=|OC|sin30°=300×=150(N),即|OB|=|AC|=150(N).则可得与铅垂线成 30°角的绳子的拉力是 150N,与铅垂线成 60°角的绳子的拉力是 150N.规律总结:解决与向量有关的实际应用题,应本着如下步骤解题:→→→→→→