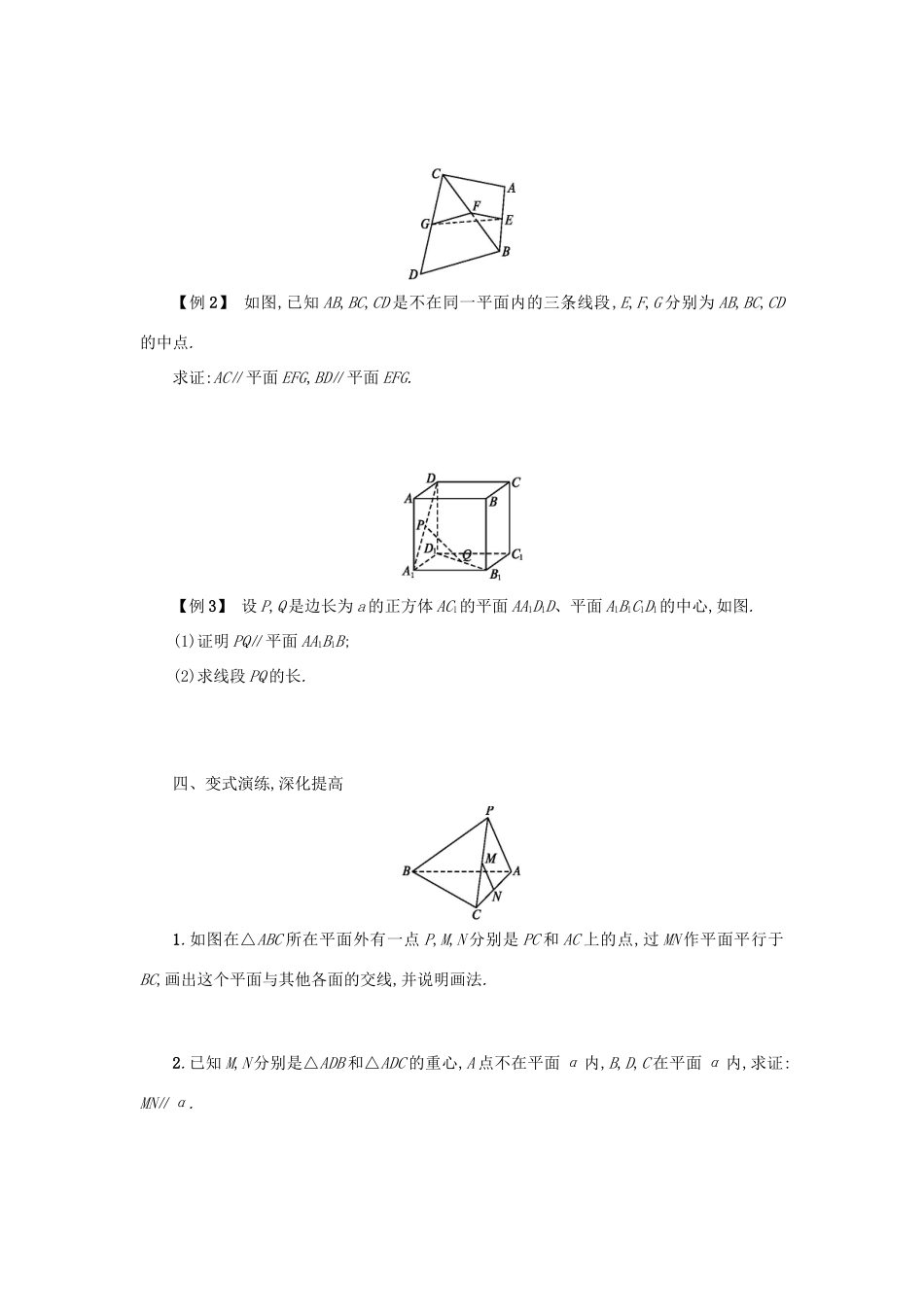
第二章 点、直线、平面之间的位置关系2.2 直线、平面平行的判定及其性质2.2.1 直线与平面平行的判定学习目标1.探究直线与平面平行的判定定理.2.直线与平面平行的判定定理的应用.合作学习一、设计问题,创设情境观察长方体,你能发现长方体 ABCD-A'B'C'D'中,线段 A'B 所在的直线与长方体 ABCD-A'B'C'D'的侧面 C'D'DC 所在平面的位置关系吗?二、信息交流,揭示规律问题 1:空间直线和平面有哪些位置关系?问题 2:直线 a 在平面 α 外,是不是能够断定 a∥α 呢?问题 3:若平面外一条直线平行于平面内一条直线,那么平面外的直线与平面的位置关系可能相交吗?问题 4:如何判定直线和平面平行?问题 5:如何证明直线与平面平行的判定定理?三、运用规律,解决问题【例 1】 求证:空间四边形相邻两边中点的连线平行于经过另外两边所在的平面.【例 2】 如图,已知 AB,BC,CD 是不在同一平面内的三条线段,E,F,G 分别为 AB,BC,CD的中点.求证:AC∥平面 EFG,BD∥平面 EFG.【例 3】 设 P,Q 是边长为 a 的正方体 AC1的平面 AA1D1D、平面 A1B1C1D1的中心,如图.(1)证明 PQ∥平面 AA1B1B;(2)求线段 PQ 的长.四、变式演练,深化提高1.如图在△ABC 所在平面外有一点 P,M,N 分别是 PC 和 AC 上的点,过 MN 作平面平行于BC,画出这个平面与其他各面的交线,并说明画法.2.已知 M,N 分别是△ADB 和△ADC 的重心,A 点不在平面 α 内,B,D,C 在平面 α 内,求证:MN∥α.五、反思小结,观点提炼请同学们回想一下,本节课我们学了哪些内容?六、作业精选,巩固提高课本 P61习题 2.2A 组第 3,4 题.参考答案二、问题 1:直线在平面内、直线与平面相交、直线与平面平行.问题 2:不能.直线 a 在平面 α 外包含两种情形:一是 a 与 α 相交,二是 a 与 α 平行,因此,由直线 a 在平面 α 外,不能断定 a∥α.问题 3:不可能相交,该直线与平面平行.问题 4:直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.进一步指出线面平行的判定定理的符号语言和图形语言.符号语言为:a⊄α,b⊂α,且 a∥b⇒a∥α.图形语言为:如图.问题 5:证明: a∥b,∴a,b 确定一个平面,设为 β.∴a⊂β,b⊂β. a⊄α,a⊂β,∴α 和 β 是两个不同平面. b⊂α 且 b⊂β,∴α∩β=b.假设 a 与 α 有公共点 P,则 P∈α∩β=b,即点 P 是 a 与 b 的公共点,这与已知 a∥b 矛盾.∴假设错误....