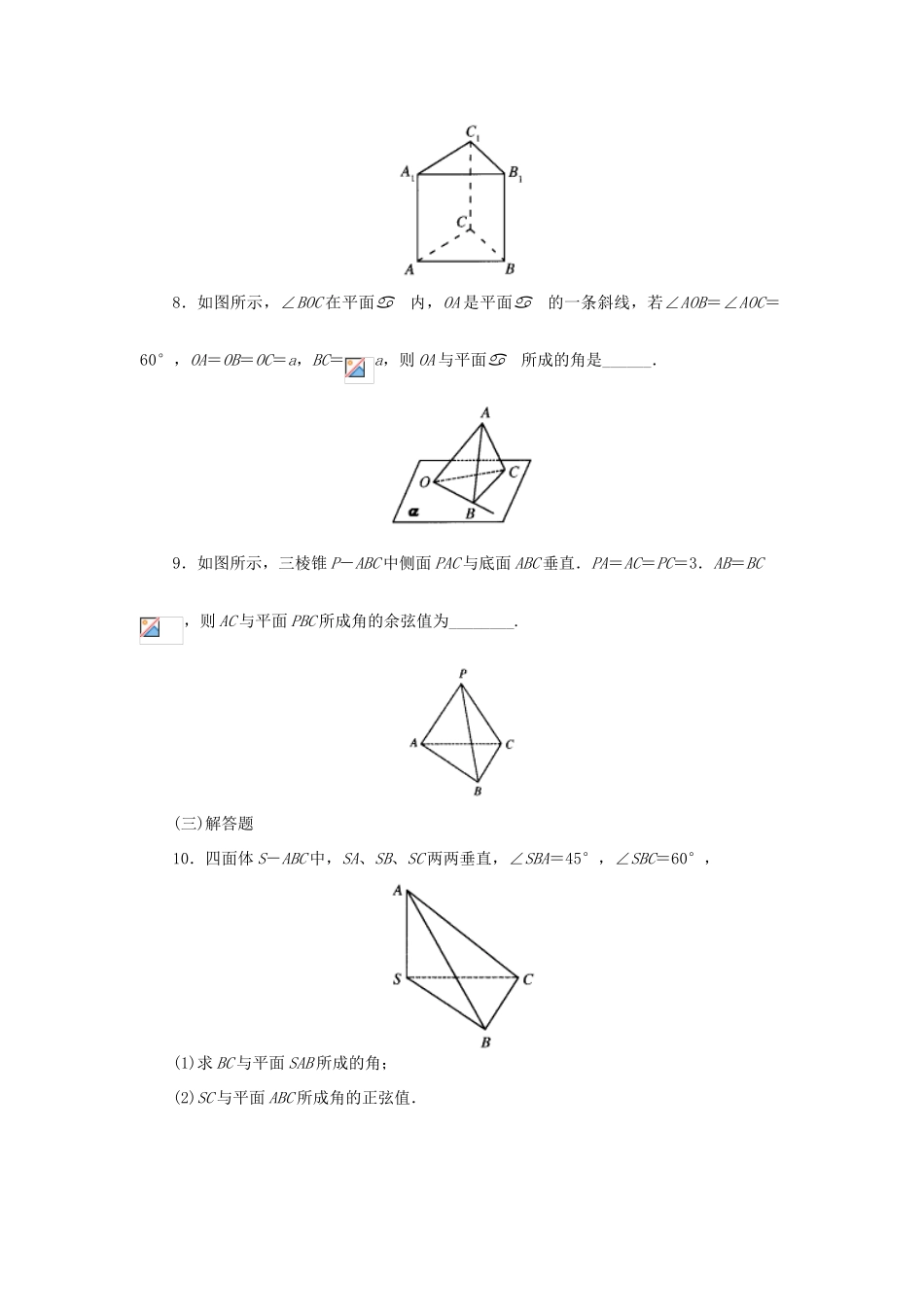
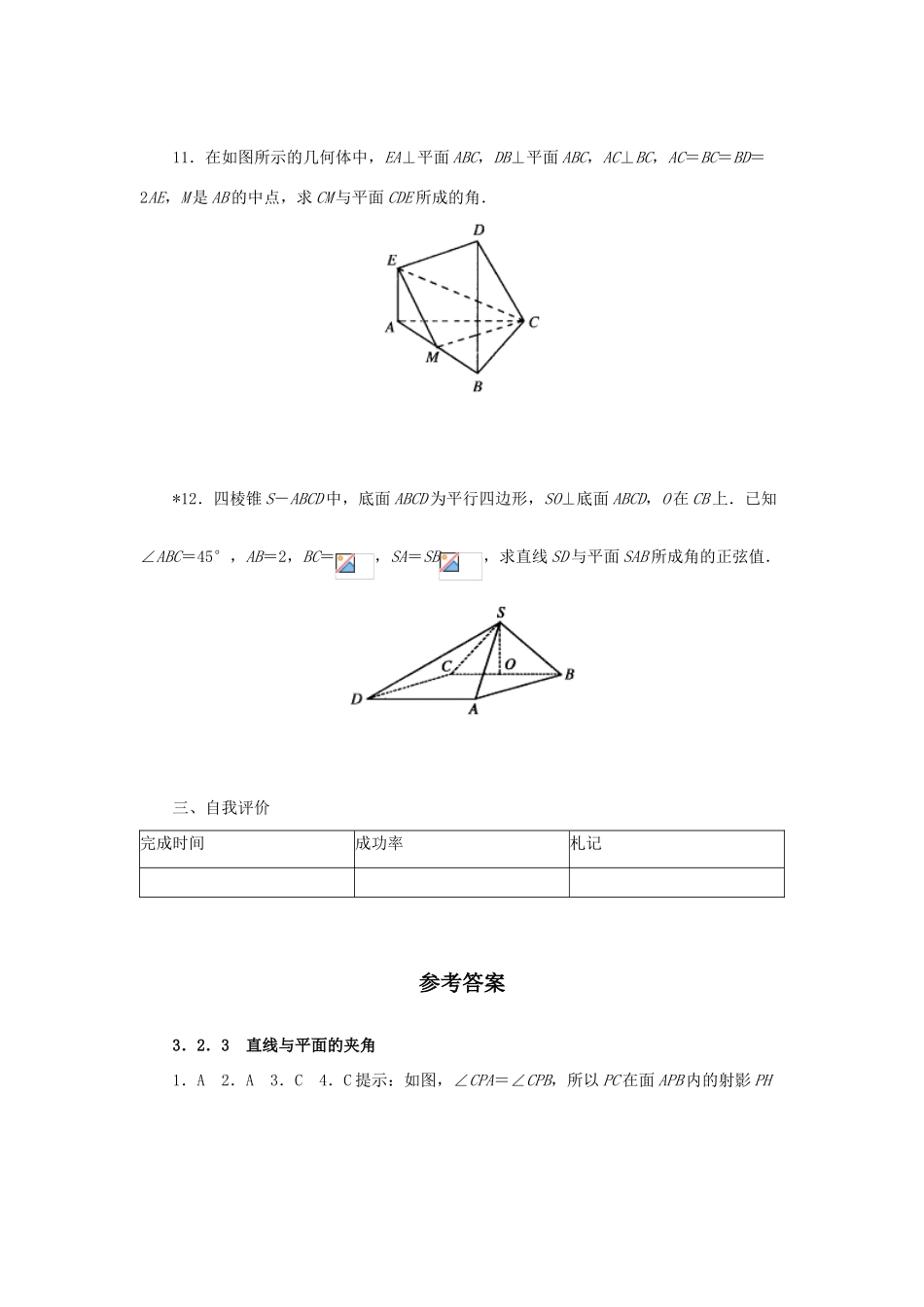
3.2.3 直线与平面的夹角一、学习目标掌握直线与平面所成的角的概念和公式,会利用向量求解线面角的大小.二、知识梳理(一)选择题(每道题的四个选择答案中有且只有一个答案是正确的)1.若斜线段 AB 是它在平面内的射影长的 2 倍,则 AB 与所成的角为( )A.60°B.45°C.30°D.120°2.矩形 ABCD 中,AB=1,,PA⊥平面 ABCD,PA=1,则 PC 与平面 ABCD 所成的角是( )A.30°B.45°C.60°D.90°3.已知长方体 ABCD-A1B1C1D1中,AB=BC=4,CC1=2,则直线 BC1和平面 DBB1D1所成角的正弦值等于( )A.B.C.D.4.PA、PB、PC 是从 P 点引出的三条射线,每两条的夹角为 60°,则直线 PC 与平面APB 所成角的余弦值为( )A.B.C.D.(二)填空题5.直角三角形 ABC 的斜边 AB 在平面内,AC 和 BC 与所成的角分别为30°,45°,CD 是 AB 边上的高,CD 与所成的角为______.*6.自平面外一点 P,向平面引垂线段 PO 及两条斜线段 PA、PB.它们在平面内的射影长分别为 2cm 和 12cm ,且这两条斜线与平面所成的角相差 45°,则垂线段 PO 的长为______.7.如图所示,在正三棱柱 ABC-A1B1C1中,侧棱长为,底面三角形的边长为 1,则BC1与侧面 ACC1A1所成的角是______.8.如图所示,∠BOC 在平面内,OA 是平面的一条斜线,若∠AOB=∠AOC=60°,OA=OB=OC=a,BC=a,则 OA 与平面所成的角是______.9.如图所示,三棱锥 P-ABC 中侧面 PAC 与底面 ABC 垂直.PA=AC=PC=3.AB=BC,则 AC 与平面 PBC 所成角的余弦值为________.(三)解答题10.四面体 S-ABC 中,SA、SB、SC 两两垂直,∠SBA=45°,∠SBC=60°,(1)求 BC 与平面 SAB 所成的角;(2)SC 与平面 ABC 所成角的正弦值.11.在如图所示的几何体中,EA⊥平面 ABC,DB⊥平面 ABC,AC⊥BC,AC=BC=BD=2AE,M 是 AB 的中点,求 CM 与平面 CDE 所成的角.*12.四棱锥 S-ABCD 中,底面 ABCD 为平行四边形,SO⊥底面 ABCD,O 在 CB 上.已知∠ABC=45°,AB=2,BC=,SA=SB,求直线 SD 与平面 SAB 所成角的正弦值.三、自我评价完成时间成功率札记参考答案3.2.3 直线与平面的夹角1.A 2.A 3.C 4.C 提示:如图,∠CPA=∠CPB,所以 PC 在面 APB 内的射影 PH是∠APB 的平分线,所以= 5.60°;6.6cm 或 4cm 提示:注...