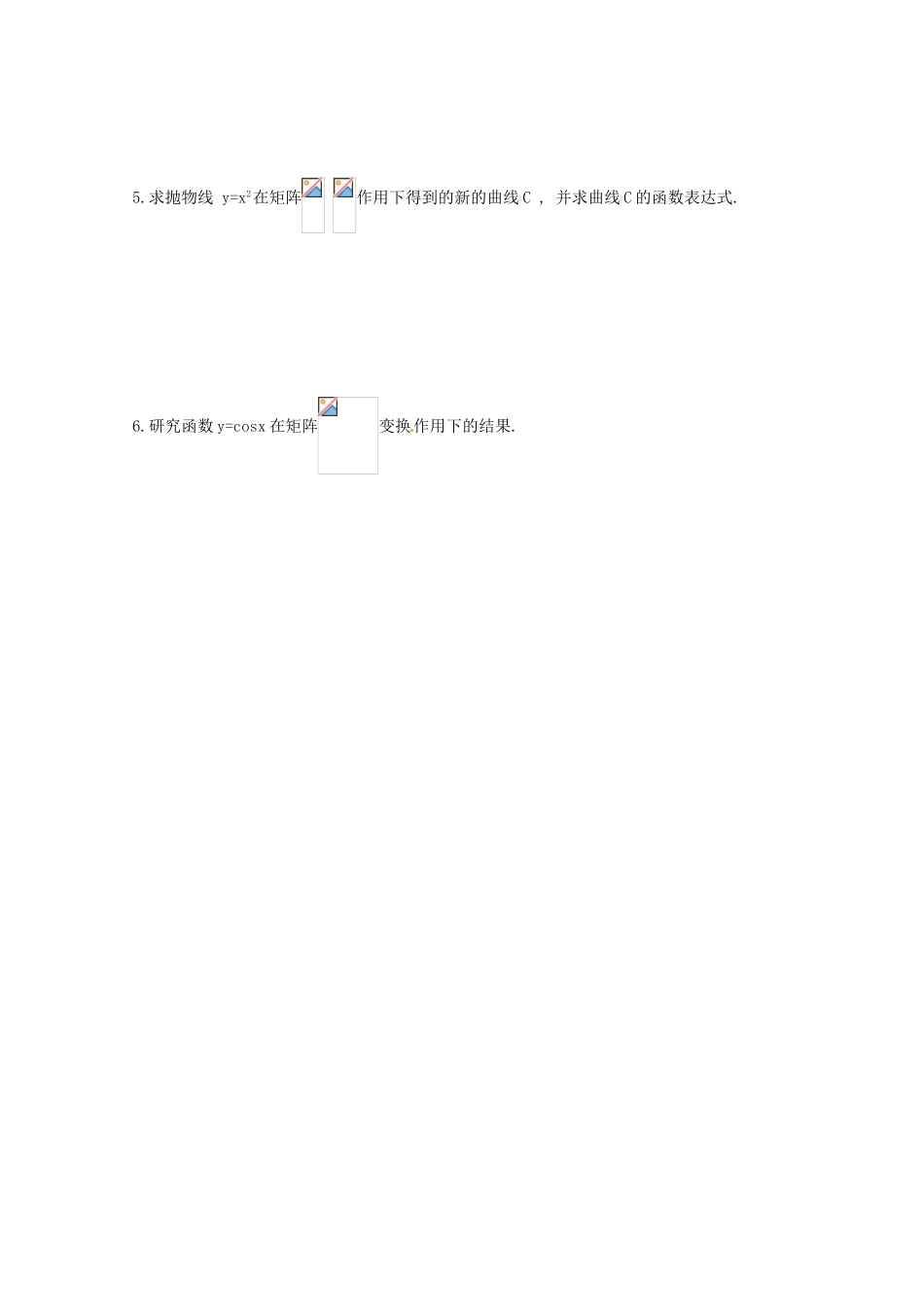
§2.2 几种常见的平面变换(1)-恒等变换、伸压变换教学目标:知识与技能:1.掌握恒等变换矩阵和伸压变换矩阵的特点.2.熟练运用恒等变换和伸压变换进行平面图形的变换过程与方法:借助立体几何图形的三视图来研究平面图形的几何变换,让学生感受具体到抽象的过程 情感、态度与价值观: 提供自主探索的空间,通过研究实例,学会从实际出发探究问题,总结过程,得出结论。教学重点:恒等变换、伸压变换的概念教学难点:恒等变换、伸压变换的矩阵教学过程:一、问题情境:已知△ABC , A(2 , 0) , B(-1 , 0) , C(0 , 2) , 它们在变换 T 作用下保持位置不变, 能否用矩阵 M 来表示这一变换?二、建构数学1.恒等变换矩阵(单位矩阵)2.恒等变换3.伸压变换矩阵4.伸压变换三、教学运用例 1、求 x2+y2=1 在矩阵 M= 作用下的图形例 2、已知曲线 y=sinx 经过变换 T 作用后变为新的曲线 C , 试求变 换 T 对应的矩阵 M , 以及曲线 C 的解析表达式.例 3、验证图 C : x2+y2=1 在矩阵 A= 对应的伸压变换下变为一个椭圆, 并求此椭圆的方程.四、课堂小结:五、课堂练习:P33 1 , 2 .六、回顾反思:七、课外作业:1.已知平行四边形 ABCD, A(-1 , 0) , B(0 , 2) , C(3 , 2) , D(0 , 2) , 它们在 变换 T作用前后保持位置不变, 则变换矩阵 M=__________ .2.已知菱形 ABCD, A(2 , 0) , B(0 , 1) , C(-2 , 0) , D(0 , -1), 在矩阵 M= 作用下变为 A′, B′, C′, D′, 求 A′, B′, C′, D′的坐标, 并画出图形.3.求△OBC 在矩阵 作用下变换的结果, 其中 O 为原点, B(-1 , 0) , C(1 , 0) .4.求正方形 A BCD 在矩阵 作用下得到的图形, 并画出示意图, 其中 A(1 , 0) , B(0 , 1) , C(-1 , 0) , D(0 , -1) .5.求抛物线 y=x2在矩阵 作用下得到的新的曲线 C , 并求曲线 C 的函数表达式.6.研究函数 y=cosx 在矩阵变换作用下的结果.