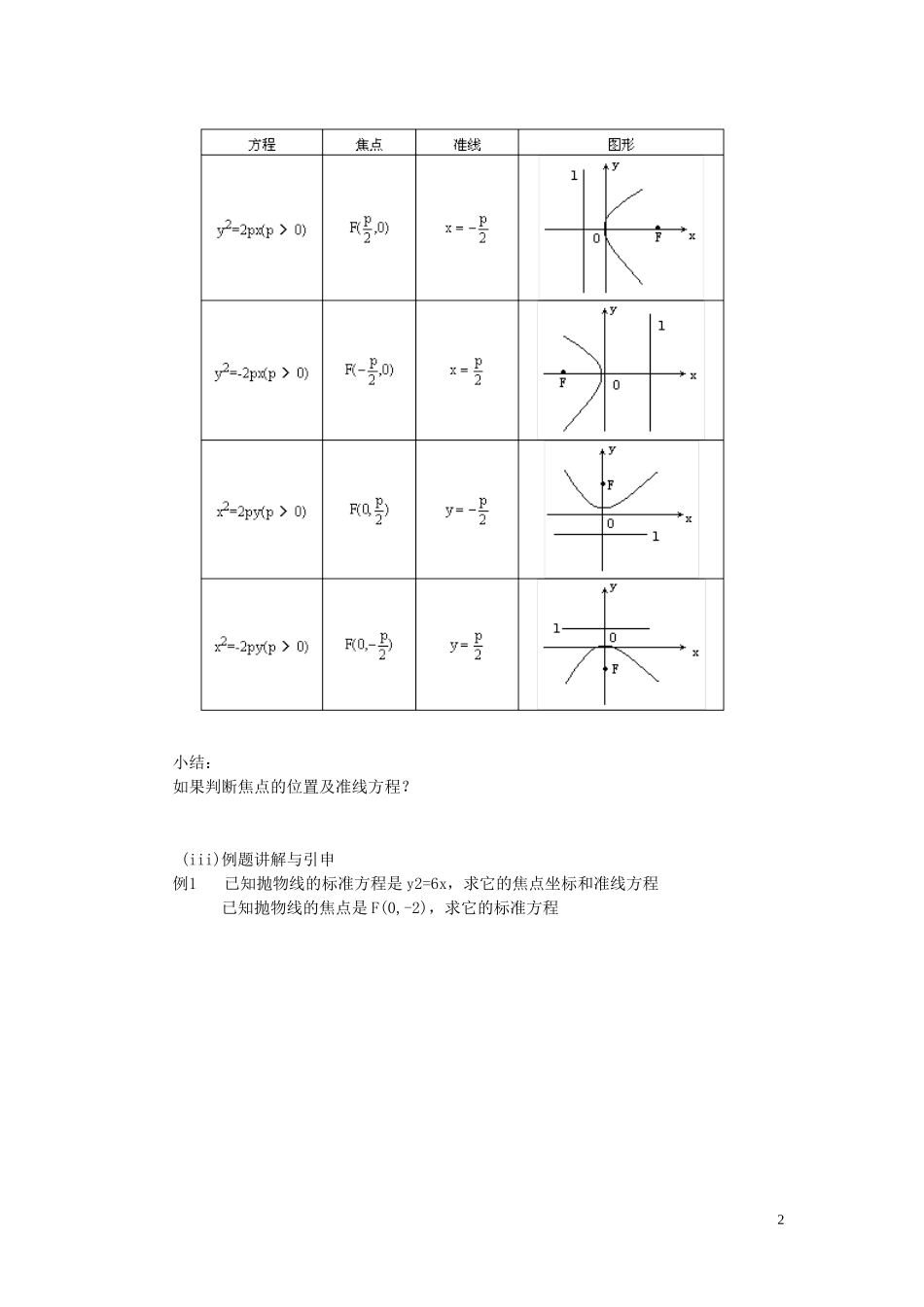
课题:抛物线及标准方程学时:09课型:新受课 (1)复习与引入过程回忆平面内与一个定点 F 的距离和一条定直线 l 的距离的比是常数 e 的轨迹,当 0<e<1 时是椭圆,当 e>1 时是双曲线,那么当 e=1 时,它又是什么曲线?2.简单实验如图 2-29,把一根直尺固定在画图板内直线 l 的位置上,一块三角板的一条直角边紧靠直尺的边缘;把一条绳子的一端固定于三角板另一条直角边上的点 A,截取绳子的长等于A 到直线 l 的距离 AC,并且把绳子另一端固定在图板上的一点 F;用一支铅笔扣着绳子,紧靠着三角板的这条直角边把绳子绷紧,然后使三角板紧靠着直尺左右滑动,这样铅笔就描出一条曲线,这条曲线叫做抛物线.反复演示后,请同学们来归纳抛物线的定义,教师总结.(2)新课讲授过程(i)由上面的探究过程得出抛物线的定义 (ii) 抛物线标准方程的推导过程由于焦点和准线在坐标系下的不同分布情况,抛物线的标准方程有四种情形(列表如下):1小结:如果判断焦点的位置及准线方程? (iii)例题讲解与引申例1已知抛物线的标准方程是 y2=6x,求它的焦点坐标和准线方程已知抛物线的焦点是 F(0,-2),求它的标准方程2例 2 一种卫星接收天线的轴截面如图所示。卫星拨束近似平行状态社如轴截面为抛物线的接受天线,经反射聚焦到焦点处。已知接收天线的口径为 4.8m 深度为 0.5m,求抛物线的标准方程和焦点坐标。课堂练习:第 67 页 1、2、3课后作业:第 73 页 1、2、3、4课后预习:双曲线的性质3