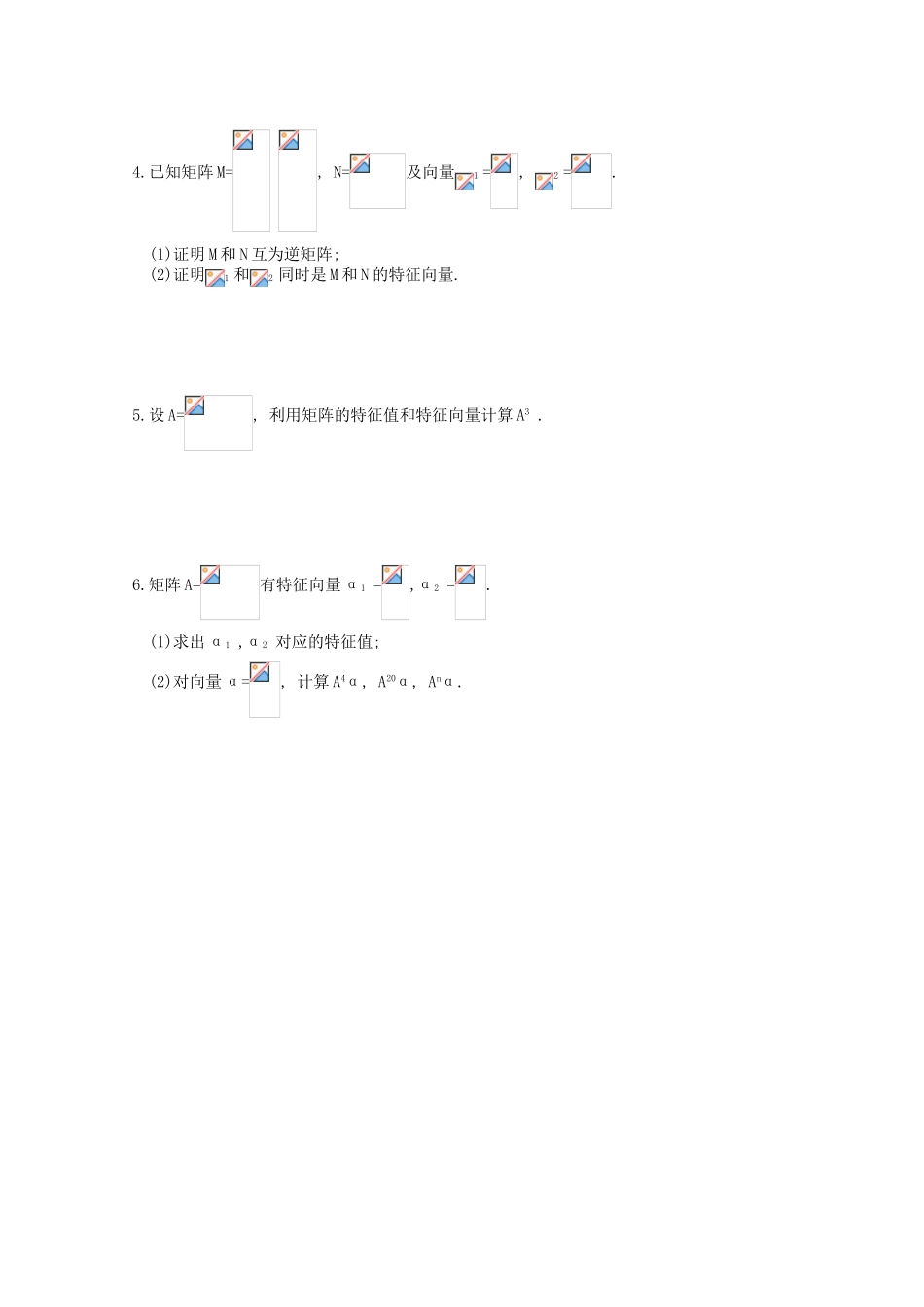
§2 矩阵与变换章节复习教学目标:知识与技能:1.对本章的知识进行归纳和梳理 2.熟练进行图形的变换和矩阵运算 3.能运用矩阵解决实际问题.过程与方法: 情感、态度与价值观: 教学重点:本章的知识教学难点:进行图形的变换和矩阵运算、能运用矩阵解决实际问题.教学过程:一、知识梳理:二、例题分析:例 1、已知 M=, 试求在 M 对应的变换 TM作用下对应得到 P(1 , 0) , Q(0 , 1)的原象点.例 2、已知. a , b∈R , 若 M= 所对应的变换 TM把直线 l: 2x-y=3 变换为自身, 求实数 a , b 的值.例 3、已知 M= , N= , J= .(1)试求满足方程 MX=N 的二阶方阵 X ; (2)试求满足方程 NYM=J 的二阶方程 Y .例 4、已知 M= 为可逆矩阵, 求 x 的取值范围及 M -1 .例 5、给定矩阵 M= 及向量 α=.(1)求 M 的特征值及对应的特征向量;(2)确定实数 a , b , 使 α=ae1+be 2 ; (3)利用(2)计算 M3α, M nα.例 6、已知点列 P1 (x1 , y1) , P2( x2 , y2), … , Pn (x n , y n ), 满足 且 x1=1 , y1=-2, n=1 , 2 , 3 , … , 问: 当 n 逐渐变大时, Pn (xn , yn)有 何变化趋势.三、课外作业:1.已知变换 T 把平面上的点(2 , -1), (-1, 2)分别变换成点(3 , -4) , (0 , 5), 试求变换 T 对应的矩阵 M .2.变换矩阵把曲线 y=lgx 变换成什么几何图形?3.判断下列矩阵是否存在逆矩阵, 若存在, 求出逆矩阵. (1) (2) (3) 4.已知矩阵 M= , N=及向量1 =, 2 =. (1)证明 M 和 N 互为逆矩阵; (2)证明1 和2 同时是 M 和 N 的特征向量.5.设 A=, 利用矩阵的特征值和特征向量计算 A3 .6.矩阵 A=有特征向量 α1 =,α2 =. (1)求出 α1 ,α2 对应的特征值; (2)对向量 α=, 计算 A4α, A20α, Anα.