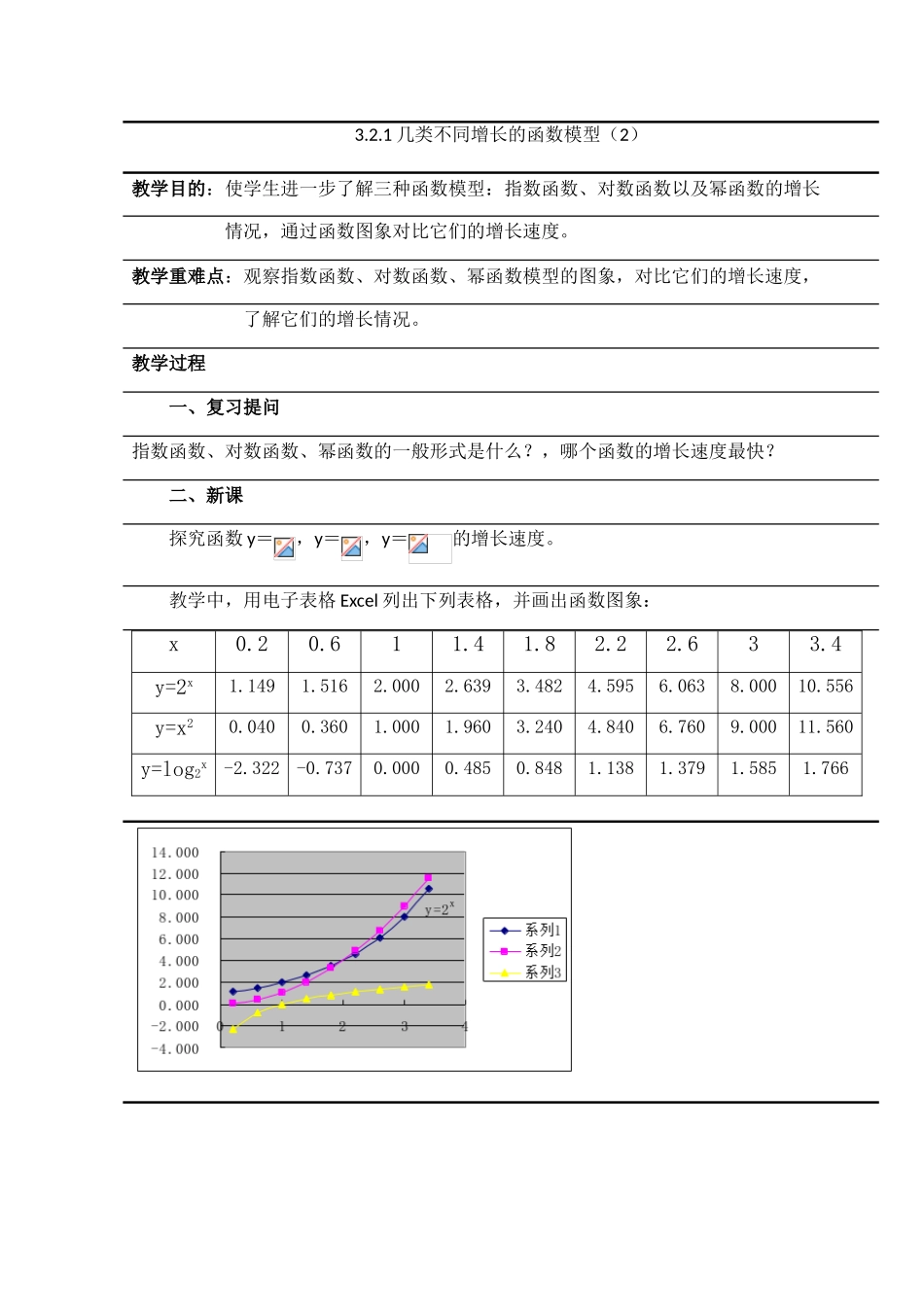
3.2.1 几类不同增长的函数模型(2)教学目的:使学生进一步了解三种函数模型:指数函数、对数函数以及幂函数的增长 情况,通过函数图象对比它们的增长速度。教学重难点:观察指数函数、对数函数、幂函数模型的图象,对比它们的增长速度,了解它们的增长情况。教学过程一、复习提问指数函数、对数函数、幂函数的一般形式是什么?,哪个函数的增长速度最快?二、新课 探究函数 y=,y=,y=的增长速度。 教学中,用电子表格 Excel 列出下列表格,并画出函数图象:x0.20.611.41.82.22.633.4y=2x1.149 1.516 2.000 2.639 3.482 4.595 6.063 8.000 10.556 y=x20.040 0.360 1.000 1.960 3.240 4.840 6.760 9.000 11.560 y=log2x-2.322 -0.737 0.000 0.485 0.848 1.138 1.379 1.585 1.766 在区间(2,4),有<<在区间(0,2)和(4,+∞)有<< 可以在更大范围内观察函数 y=,y=的图象的增长情况。 一般地,对于指数函数 y=(a>1)和幂函数 y=(n>0),通过探索可以发现,在区间(0,+∞)上,无论 n 比 a 大多少,尽管 x 在一定范围内,会小于但由于的增长速度快于,因此总存在一个,当 x>时,就会有>。 同样地,对于对数函数 y=(a>1)和幂函数 y=(n>0),在区间(0,+∞)上,随着 x 的增大,增长得越来越慢,图象就像是渐渐地与 x 轴平行一样。尽管 x 在一定范围内,可能会大于,但由于的增长慢于,因此总存在一个,当 x>时,就会有<。 综上所述,在区间(0,+∞)上,尽管函数 y=(a>1)、y=(a>1)和 y=(n>0)都是增函数。但它们的增长速度不同,而且不在同一个“档次”上随着 x 的增大,y=(a>1)的增长速度越来越快,会超过并远远大于 y=(n>0)的增长速度,而 y=(a>1)的增长速度越来越慢。因此总存在一个,当 x>时,<<。练习:P119作业:P127 3、4