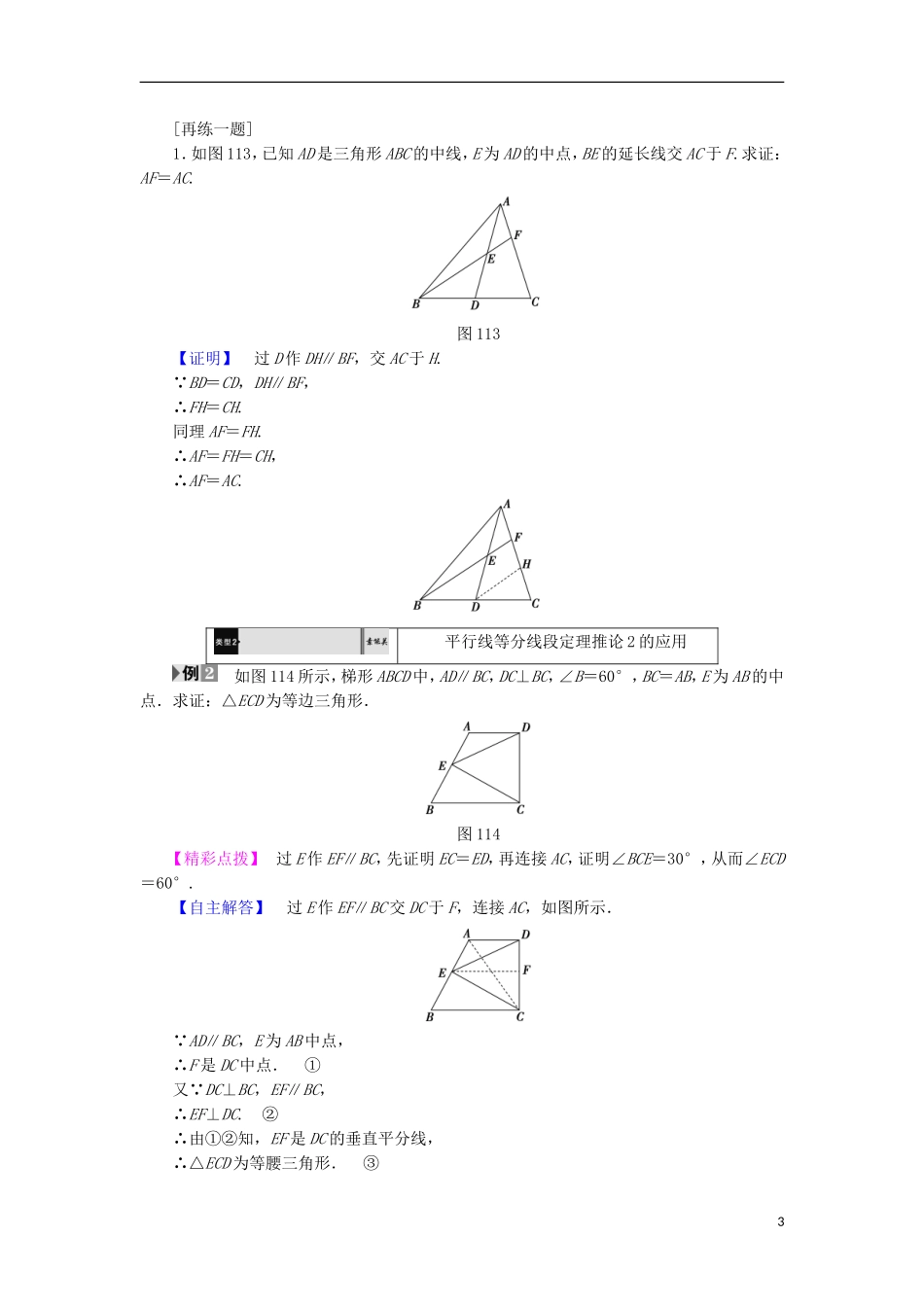
一 平行线等分线段定理1.掌握平行线等分线段定理及其两个推论.(重点)2.能运用平行线等分线段定理及其两个推论进行简单的证明或计算.(难点)[基础·初探]教材整理 1 平行线等分线段定理阅读教材 P2~P3定理以上部分,完成下列问题.1.文字语言如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.2.图形语言如图 111,l1∥l2∥l3,l 分别交 l1,l2,l3于 A,B,C,l′分别交 l1,l2,l3于 A1,B1,C1,若 AB=BC,则 A1B1= B 1C1.图 111教材整理 2 平行线等分线段定理的推论阅读教材 P4~P5“习题”以上部分,完成下列问题.1.推论 1经过三角形一边的中点与另一边平行的直线必平分第三边.2.推论 2经过梯形一腰的中点,且与底边平行的直线平分另一腰.在梯形 ABCD 中,M,N 分别是腰 AB 与腰 CD 的中点,且 AD=2,BC=4,则 MN 等于( )【导学号:07370000】A.2.5 B.3C.3.5 D.不确定【解析】 由梯形中位线定理知选B.【答案】 B1[质疑·手记]预习完成后,请将你的疑问记录,并与“小伙伴们”探讨交流:疑问 1: 解惑: 疑问 2: 解惑: 疑问 3: 解惑: [小组合作型]平行线等分线段定理推论 1 的应用 如图 112,在△ABC 中,AD,BF 为中线,AD,BF 交于 G,CE∥FB 交 AD 的延长线于 E.求证:AG=2DE.图 112【精彩点拨】 →→→【自主解答】 在△AEC 中, AF=FC,GF∥EC,∴AG=GE. CE∥FB,∴∠GBD=∠ECD,∠BGD=∠E.又 BD=DC,∴△BDG≌△CDE.故 DG=DE,即 GE=2DE,因此 AG=2DE.1.如果已知条件中出现中点,往往运用三角形的中位线定理来解决问题.2.本例在证明 DG=DE 时也可以过 D 作 EC 的平行线 DH.因为 BG∥DH∥CE 且 BD=CD 得 DG=DE,使用平行线等分线段定理来证明.2[再练一题]1.如图 113,已知 AD 是三角形 ABC 的中线,E 为 AD 的中点,BE 的延长线交 AC 于 F.求证:AF=AC.图 113【证明】 过 D 作 DH∥BF,交 AC 于 H. BD=CD,DH∥BF,∴FH=CH.同理 AF=FH.∴AF=FH=CH,∴AF=AC. 平行线等分线段定理推论 2 的应用 如图 114 所示,梯形 ABCD 中,AD∥BC,DC⊥BC,∠B=60°,BC=AB,E 为 AB 的中点.求证:△ECD 为等边三角形.图 114【精彩点拨】 过 E 作 EF∥BC,先证明 EC=ED,再连接 AC,证明∠BCE=30°,从而∠ECD=60°.【自主解答】 过 E ...