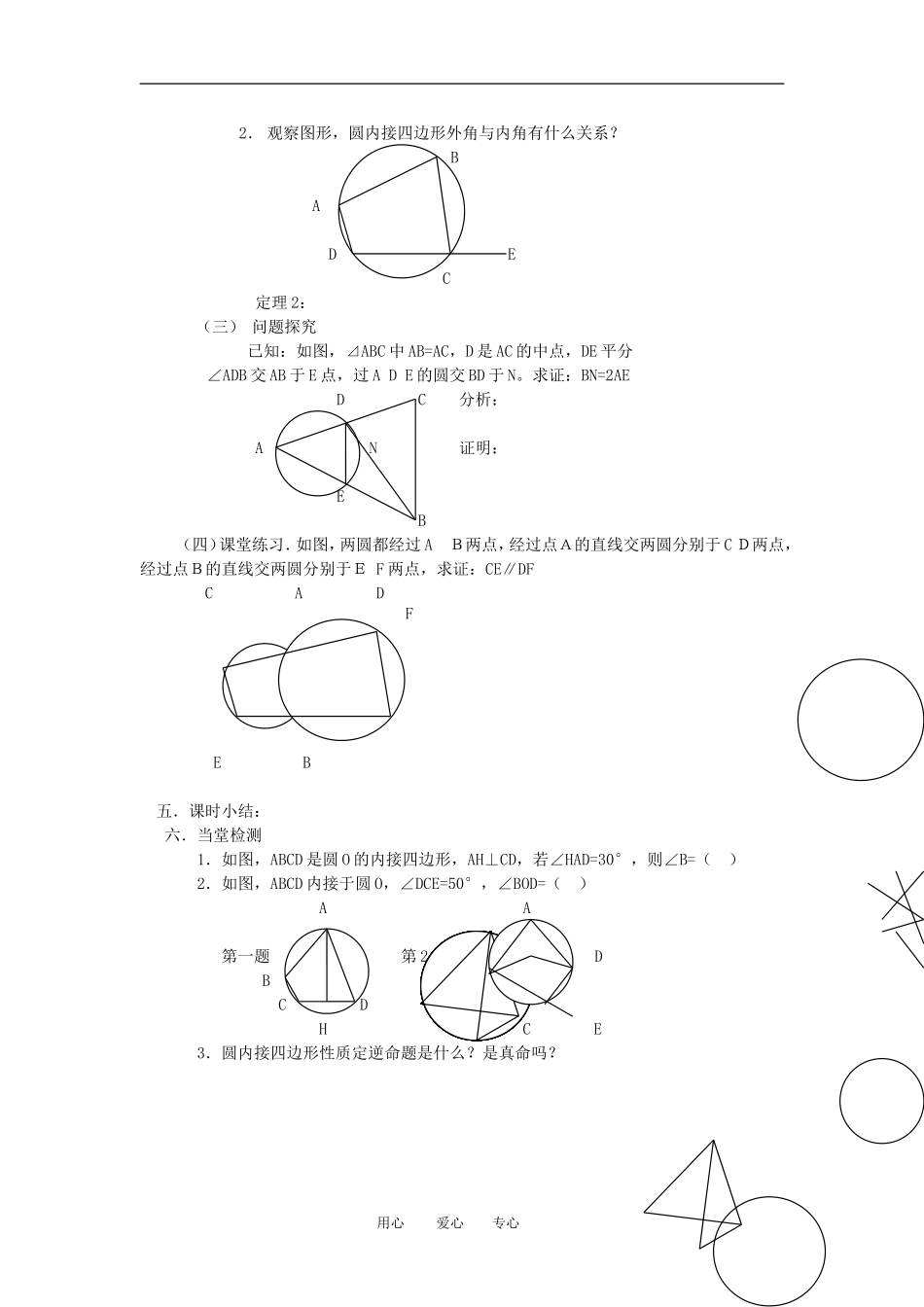
导学案:圆内接四边形的性质 高二数学组一.三维目标:1. 知识与技能:通过观察 测量 猜想获得圆内接四边形的性质定理,然后进行严格的推理论证。2. 过程与方法:探究圆内接四边形的性质定理,感知蕴涵在探求过程中的数学思想方法。3. 情感 态度与价值观:本节启发我们在研究问题时要抓住本质,严谨细致思考,规范得出结论的合理推理能力和概括能力。二.重点与难点:1. 圆内接四边形性质定理及其证明。2. 本节内容中蕴涵的数学思想和方法。三.学习流程:圆内接四边形概念---观察 测量一组图形---探究圆内接四边形性质定理并证明---应用举例---小结 练习四.导学过程:(一) 自主学习1. 什么是圆内接多边形?2. 任意三角形都有外接圆,该圆有什么特点?3. 任意正方形都有外接圆吗?4. 矩形有外接圆吗?为什么?5. 一般的四边形存在外接圆吗?(二) 合作学习1. 观察下列图形,这些四边形都内接于圆,你能发现它们的共同特征吗?共同特征是:( )猜想:圆内接四边形的( ),你能证明吗?如图,已知:四边形 ABCD 内接于圆 O,求证:∠A+∠C=180° 证明: A B O D C 定理 1: 用心 爱心 专心12. 观察图形,圆内接四边形外角与内角有什么关系? B A D E C定理 2:(三) 问题探究 已知:如图,⊿ABC 中 AB=AC,D 是 AC 的中点,DE 平分∠ADB 交 AB 于 E 点,过 A D E 的圆交 BD 于 N。求证:BN=2AE D C 分析: A N 证明: E B (四)课堂练习.如图,两圆都经过 A B两点,经过点A的直线交两圆分别于 C D两点,经过点B的直线交两圆分别于E F 两点,求证:CE∥DF C A DFE B 五.课时小结: 六.当堂检测 1.如图,ABCD 是圆 O 的内接四边形,AH⊥CD,若∠HAD=30°,则∠B=( ) 2.如图,ABCD 内接于圆 O,∠DCE=50°,∠BOD=( ) A A 第一题 第 2 题 D BB C D H CE 3.圆内接四边形性质定逆命题是什么?是真命吗?用心 爱心 专心2