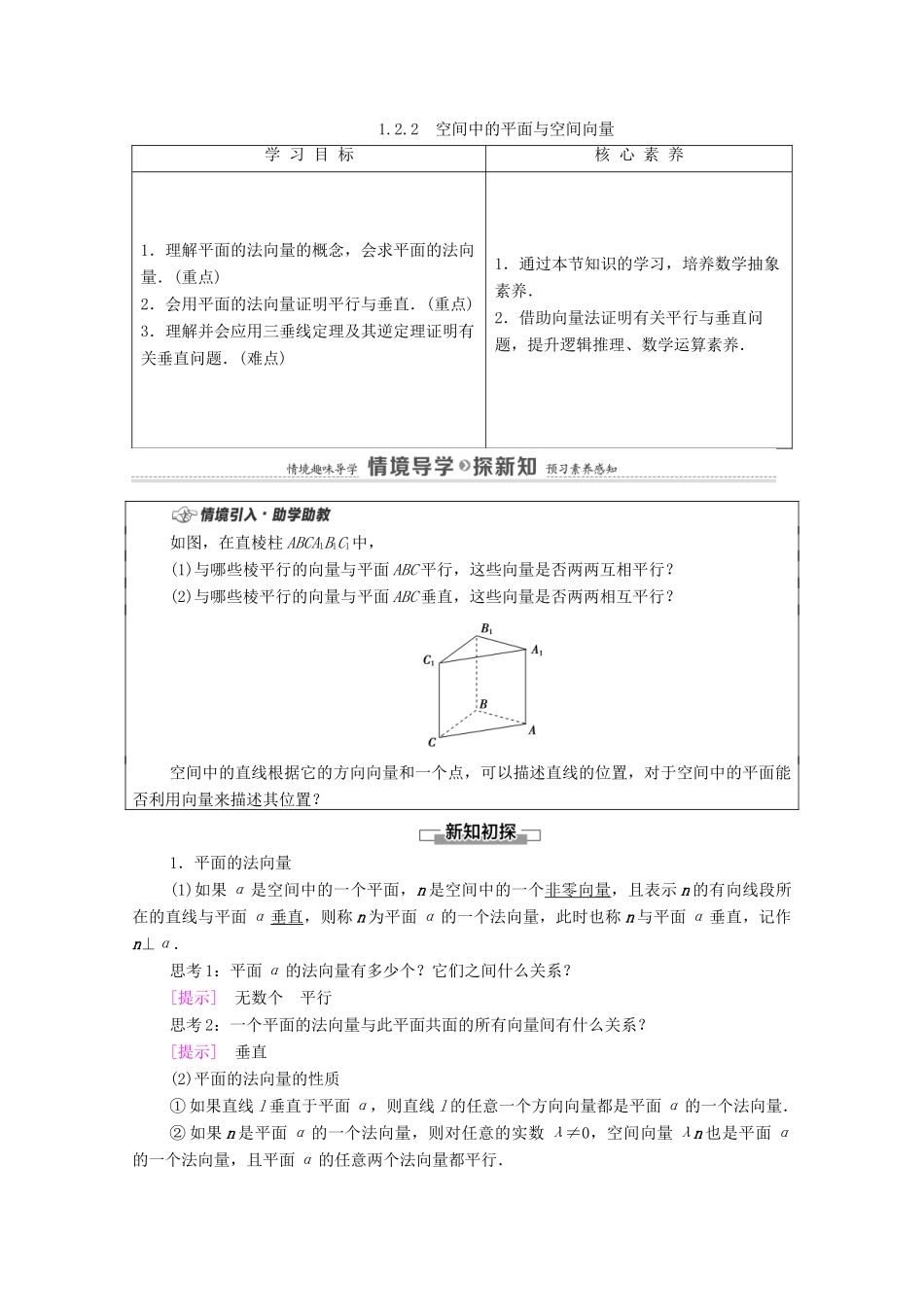
1.2.2 空间中的平面与空间向量学 习 目 标核 心 素 养1.理解平面的法向量的概念,会求平面的法向量.(重点)2.会用平面的法向量证明平行与垂直.(重点)3.理解并会应用三垂线定理及其逆定理证明有关垂直问题.(难点)1.通过本节知识的学习,培养数学抽象素养.2.借助向量法证明有关平行与垂直问题,提升逻辑推理、数学运算素养.如图,在直棱柱 ABCA1B1C1中,(1)与哪些棱平行的向量与平面 ABC 平行,这些向量是否两两互相平行?(2)与哪些棱平行的向量与平面 ABC 垂直,这些向量是否两两相互平行?空间中的直线根据它的方向向量和一个点,可以描述直线的位置,对于空间中的平面能否利用向量来描述其位置? 1.平面的法向量(1)如果 α 是空间中的一个平面,n 是空间中的一个非零向量,且表示 n 的有向线段所在的直线与平面 α 垂直,则称 n 为平面 α 的一个法向量,此时也称 n 与平面 α 垂直,记作n⊥α.思考 1:平面 α 的法向量有多少个?它们之间什么关系?[提示] 无数个 平行思考 2:一个平面的法向量与此平面共面的所有向量间有什么关系?[提示] 垂直(2)平面的法向量的性质① 如果直线 l 垂直于平面 α,则直线 l 的任意一个方向向量都是平面 α 的一个法向量.② 如果 n 是平面 α 的一个法向量,则对任意的实数 λ≠0,空间向量 λn 也是平面 α的一个法向量,且平面 α 的任意两个法向量都平行.③ 如果 n 为平面 α 的一个法向量,A 为平面 α 上一个已知的点,则对于平面 α 上任意一点 B,向量AB一定与向量 n 垂直,即 n·AB=0,从而可知平面 α 的位置可由 n 和 A 唯一确定.(3) 如 果 v 是 直 线 l 的 一 个 方 向 向 量 , n 是 平 面 α 的 一 个 法 向 量 , 则n∥v⇔l ⊥ α ,n⊥v⇔l ∥ α ,或 l ⊂ α .(4) 如 果 n1 是 平 面 α1 的 一 个 法 向 量 , n2 是 平 面 α2 的 一 个 法 向 量 , 则n1⊥n2⇔α1⊥ α 2,n1∥n2⇔α1∥α2或 α1与 α2重合.2.三垂线定理及其逆定理(1)三垂线定理:如果平面内的一条直线与平面的一条斜线在该平面内的射影垂直,则它也和这条斜线垂直.(2)三垂线定理的逆定理:如果平面内的一条直线和这个平面的一条斜线垂直,则它也和这条斜线在该平面内的射影垂直.提醒:定理中的已知直线必须是已知平面内的直线.1.思考辨析(正确的打...