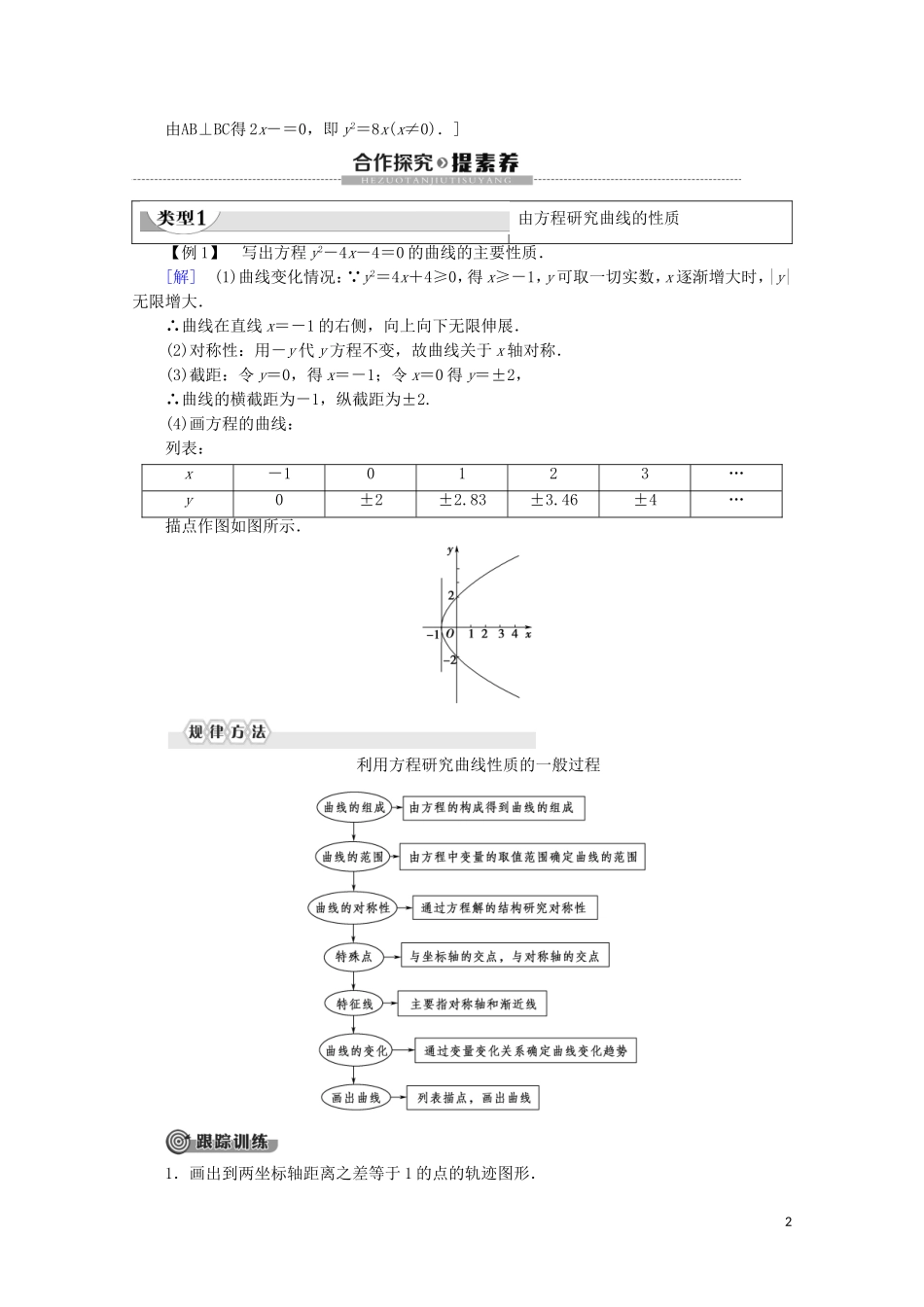
2.1.2 由曲线求它的方程、由方程研究曲线的性质学 习 目 标核 心 素 养1.掌握求轨迹方程建立坐标系的一般方法,熟悉求曲线方程的五个步骤.2.掌握求轨迹方程的几种常用方法.(重点、难点)3.初步学会通过曲线的方程研究曲线的几何性质.1.通过由方程研究曲线的性质,培养学生直观想象素养.2.借助由曲线求它的方程,提升学生逻辑推理、数学运算素养.1.解析几何研究的主要问题(1)由曲线求它的方程.(2)利用方程研究曲线的性质.2.求曲线的方程的步骤思考:求曲线方程的步骤是否可以省略.[提示] 可以省略.如果化简前后方程的解集是相同的,可以省略步骤“证明”,如有特殊情况,可以适当说明.1.已知等腰三角形 ABC 底边两端点是 A(-,0),B(,0),顶点 C 的轨迹是( )A.一条直线 B.一条直线去掉一点C.一个点 D.两个点B [C 的轨迹是线段 AB 的垂直平分线去掉 AB 的中点.]2.已知点 A(-2,0),B(2,0),C(0,3),则△ABC 底边 AB 的中线的方程是( )A.x=0 B.x=0(0≤y≤3)C.y=0 D.y=0(0≤x≤2)[答案] B3.平面上有三点 A(-2,y),B,C(x,y),若AB⊥BC,则动点 C 的轨迹方程为________.y2=8x(x≠0) [AB=,BC=,1由AB⊥BC得 2x-=0,即 y2=8x(x≠0).]由方程研究曲线的性质【例 1】 写出方程 y2-4x-4=0 的曲线的主要性质.[解] (1)曲线变化情况: y2=4x+4≥0,得 x≥-1,y 可取一切实数,x 逐渐增大时,|y|无限增大.∴曲线在直线 x=-1 的右侧,向上向下无限伸展.(2)对称性:用-y 代 y 方程不变,故曲线关于 x 轴对称.(3)截距:令 y=0,得 x=-1;令 x=0 得 y=±2,∴曲线的横截距为-1,纵截距为±2.(4)画方程的曲线: 列表: x-10123…y0±2±2.83±3.46±4…描点作图如图所示.利用方程研究曲线性质的一般过程1.画出到两坐标轴距离之差等于 1 的点的轨迹图形.2[解] 到两坐标轴距离之差等于 1 的点(x,y),满足的方程是||x|-|y||=1,其中以-x 代 x,或-y 代 y,方程都不变,所以方程的曲线关于坐标轴对称,同时也关于原点对称,需画出 x≥0,y≥0 的图形后,利用对称性完成画图,如图.直接法求曲线方程【例 2】 已知一条直线 l 和它上方的一个点 F,点 F 到 l 的距离是 2.一条曲线也在 l 的上方,它上面的每一点到 F 的距离减去到 l 的距离的差都是 2,建立适当的坐标系,求这条曲线的方程.[思路探究] 由条件可知...