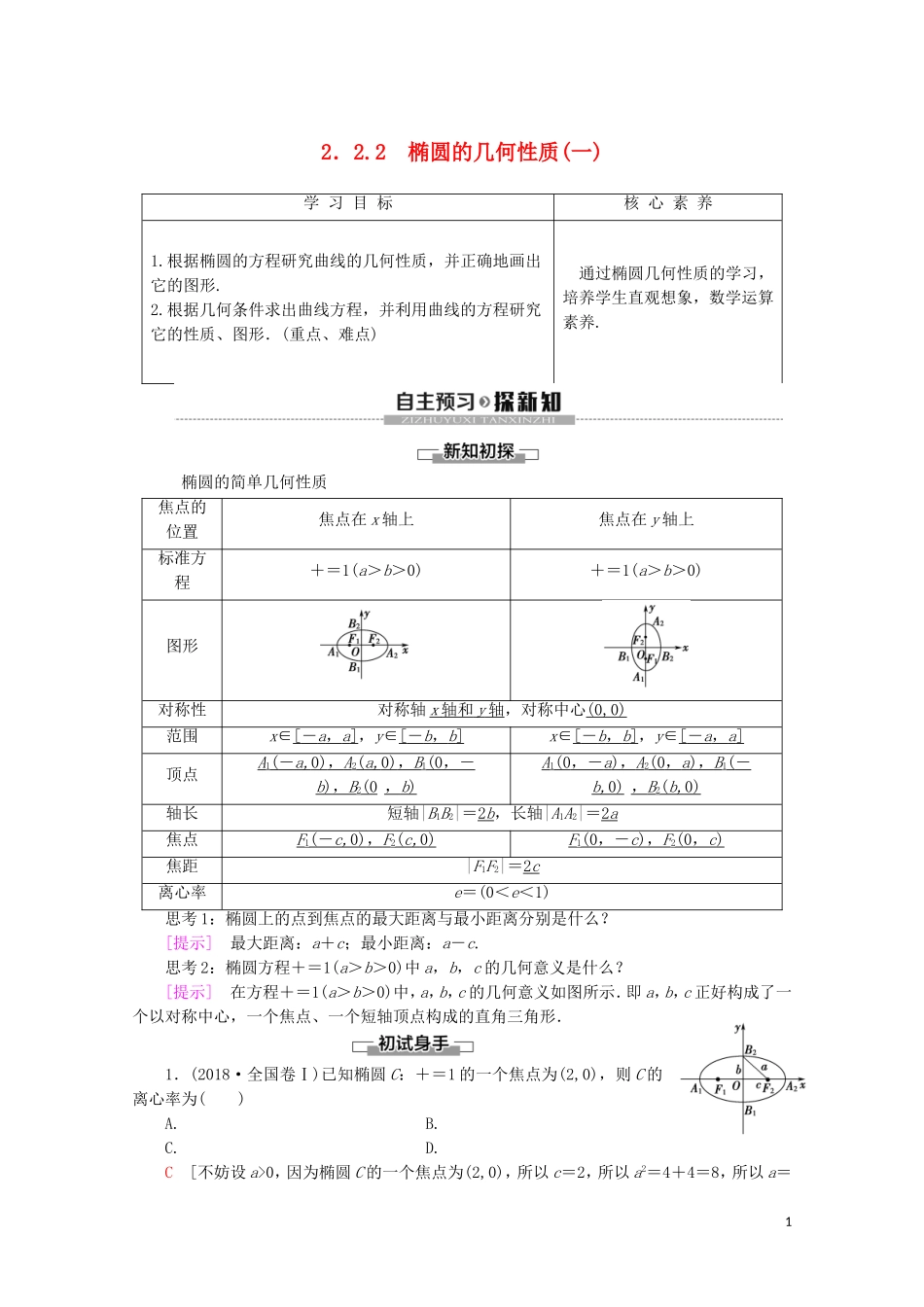
2.2.2 椭圆的几何性质(一)学 习 目 标核 心 素 养1.根据椭圆的方程研究曲线的几何性质,并正确地画出它的图形.2.根据几何条件求出曲线方程,并利用曲线的方程研究它的性质、图形.(重点、难点) 通过椭圆几何性质的学习,培养学生直观想象,数学运算素养. 椭圆的简单几何性质焦点的位置焦点在 x 轴上焦点在 y 轴上标准方程+=1(a>b>0)+=1(a>b>0)图形对称性对称轴 x 轴和 y 轴 ,对称中心(0,0)范围x∈[ - a , a ] ,y∈[ - b , b ] x∈[ - b , b ] ,y∈[ - a , a ] 顶点A1( - a, 0) , A 2( a, 0) , B 1(0 ,- b ) , B 2(0 , b ) A1(0 ,- a ) , A 2(0 , a ) , B 1( - b, 0) , B 2( b, 0) 轴长短轴|B1B2|=2 b ,长轴|A1A2|=2 a 焦点F1( - c, 0) , F 2( c, 0) F1(0 ,- c ) , F 2(0 , c ) 焦距|F1F2|=2 c 离心率e=(0<e<1)思考 1:椭圆上的点到焦点的最大距离与最小距离分别是什么?[提示] 最大距离:a+c;最小距离:a-c.思考 2:椭圆方程+=1(a>b>0)中 a,b,c 的几何意义是什么?[提示] 在方程+=1(a>b>0)中,a,b,c 的几何意义如图所示.即 a,b,c 正好构成了一个以对称中心,一个焦点、一个短轴顶点构成的直角三角形.1.(2018·全国卷Ⅰ)已知椭圆 C:+=1 的一个焦点为(2,0),则 C 的离心率为( )A. B.C. D.C [不妨设 a>0,因为椭圆 C 的一个焦点为(2,0),所以 c=2,所以 a2=4+4=8,所以 a=12,所以椭圆 C 的离心率 e==.]2.椭圆 6x2+y2=6 的长轴端点坐标为( )A.(-1,0)(1,0) B.(-6,0),(6,0)C.(-,0),(,0) D.(0,-),(0,)D [x2+=1 焦点在 y 轴上,长轴端点坐标为(0,-),(0,).]3.椭圆+=1 的焦距为 2,则 m=________.3 或 5 [由题意得 c=1,当焦点在 x 轴上时,m-4=1 得 m=5,当焦点在 y 轴上时,4-m=1 解得 m=3.]由椭圆方程求椭圆的几何性质【例 1】 求椭圆 16x2+25y2=400 的长轴和短轴的长、离心率、焦点和顶点的坐标.[思路探究] 化为标准方程,确定焦点位置及 a,b,c 的值,再研究相应的几何性质.[解] 把已知方程化成标准方程+=1,可知 a=5,b=4,所以 c=3.因此,椭圆的长轴和短轴的长分别是 2a=10 和 2b=8,离心率 e==,两个焦点分别是 F1(-3,0)和 ...