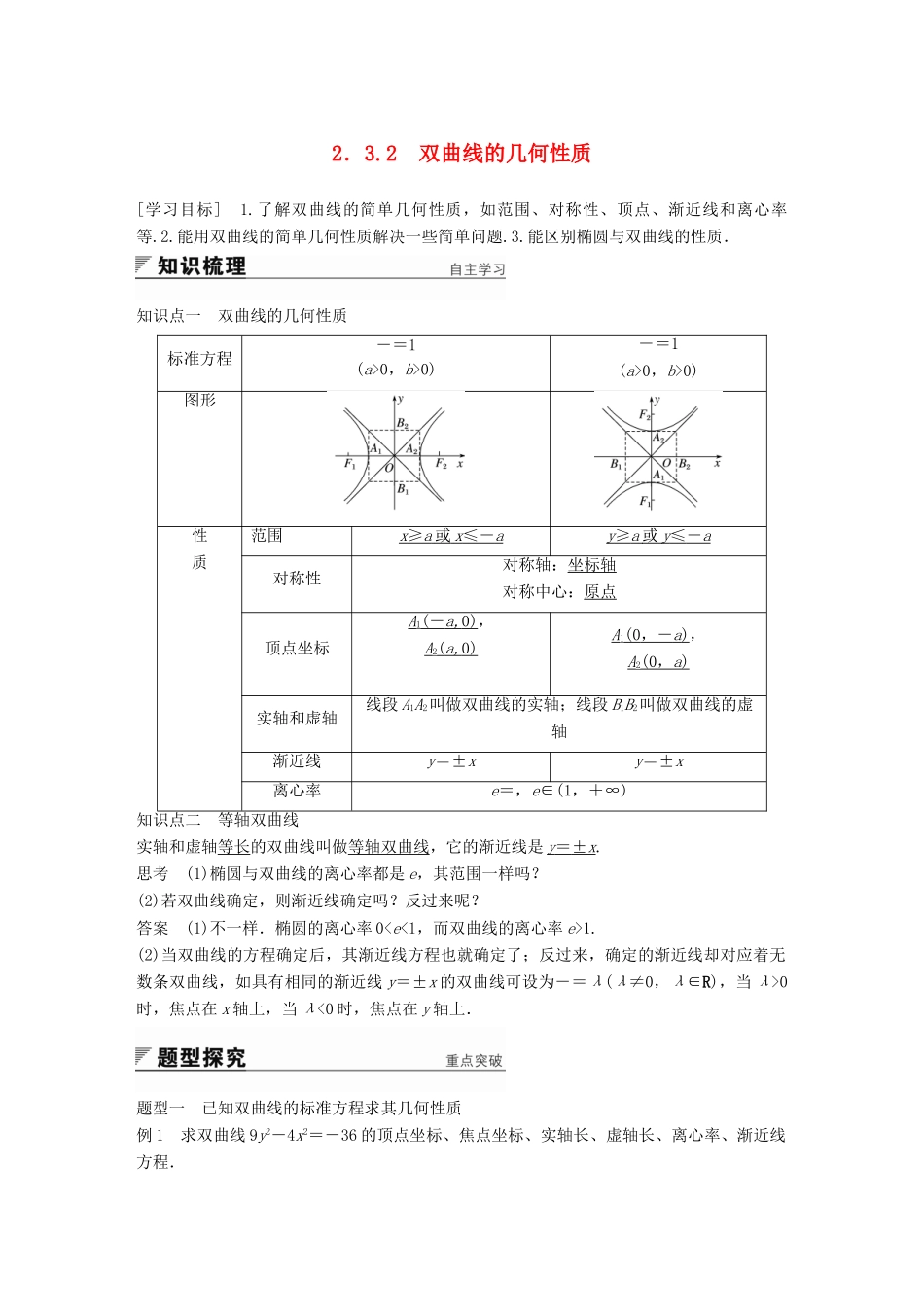
2.3.2 双曲线的几何性质[学习目标] 1.了解双曲线的简单几何性质,如范围、对称性、顶点、渐近线和离心率等.2.能用双曲线的简单几何性质解决一些简单问题.3.能区别椭圆与双曲线的性质.知识点一 双曲线的几何性质标准方程-=1(a>0,b>0)-=1(a>0,b>0)图形性质范围x ≥ a 或 x ≤ - a y ≥ a 或 y ≤ - a 对称性对称轴:坐标轴对称中心:原点顶点坐标A1( - a, 0) ,A2( a, 0) A1(0 ,- a ) ,A2(0 , a ) 实轴和虚轴线段 A1A2叫做双曲线的实轴;线段 B1B2叫做双曲线的虚轴渐近线y=±xy=±x离心率e=,e∈(1,+∞)知识点二 等轴双曲线实轴和虚轴等长的双曲线叫做等轴双曲线,它的渐近线是 y = ± x .思考 (1)椭圆与双曲线的离心率都是 e,其范围一样吗?(2)若双曲线确定,则渐近线确定吗?反过来呢?答案 (1)不一样.椭圆的离心率 01.(2)当双曲线的方程确定后,其渐近线方程也就确定了;反过来,确定的渐近线却对应着无数条双曲线,如具有相同的渐近线 y=±x 的双曲线可设为-=λ(λ≠0,λ∈R),当 λ>0时,焦点在 x 轴上,当 λ<0 时,焦点在 y 轴上.题型一 已知双曲线的标准方程求其几何性质例 1 求双曲线 9y2-4x2=-36 的顶点坐标、焦点坐标、实轴长、虚轴长、离心率、渐近线方程.解 将 9y2-4x2=-36 化为标准方程-=1,即-=1,∴a=3,b=2,c=.因此顶点为 A1(-3,0),A2(3,0),焦点为 F1(-,0),F2(,0),实轴长 2a=6,虚轴长 2b=4,离心率 e==,渐近线方程为 y=±x=±x.反思与感悟 讨论双曲线的几何性质,先要将双曲线方程化为标准形式,然后根据双曲线两种形式的特点得到几何性质.跟踪训练 1 求双曲线 x2-3y2+12=0 的实轴长、虚轴长、焦点坐标、顶点坐标、渐近线方程、离心率.解 将方程 x2-3y2+12=0 化为标准方程-=1,∴a2=4,b2=12,∴a=2,b=2,∴c===4.∴双曲线的实轴长 2a=4,虚轴长 2b=4.焦点坐标为 F1(0,-4),F2(0,4),顶点坐标为 A1(0,-2),A2(0,2),渐近线方程为 y=±x,离心率 e=2.题型二 根据双曲线的几何性质求标准方程例 2 求适合下列条件的双曲线的标准方程:(1)一个焦点为(0,13),且离心率为;(2)渐近线方程为 y=±x,且经过点 A(2,-3).解 (1)依题意可知,双曲线的焦点在 y 轴上,且 c=13,又=,∴a=5,b==12,故其标准方程为-=1...