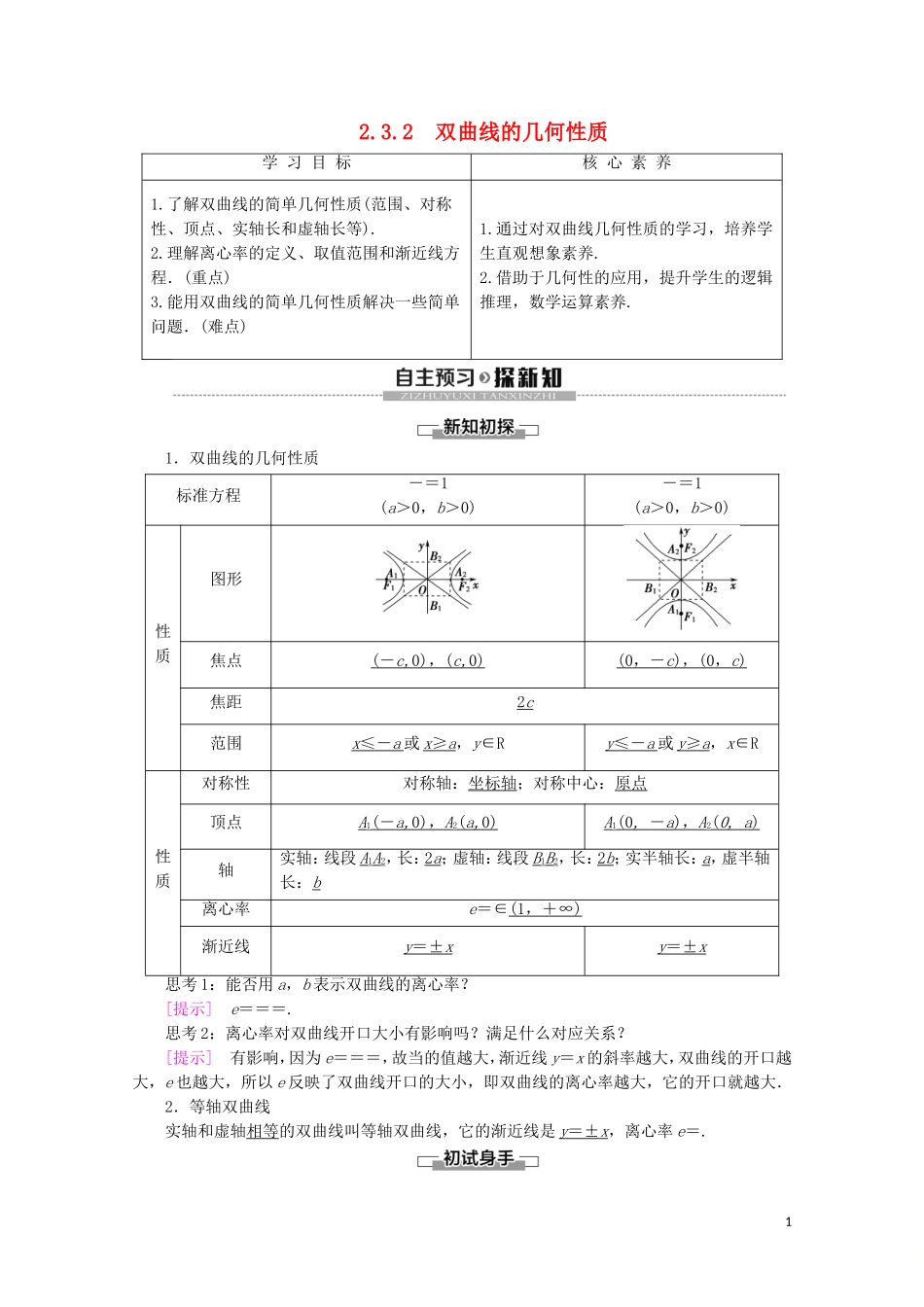
2.3.2 双曲线的几何性质学 习 目 标核 心 素 养1.了解双曲线的简单几何性质(范围、对称性、顶点、实轴长和虚轴长等).2.理解离心率的定义、取值范围和渐近线方程.(重点)3.能用双曲线的简单几何性质解决一些简单问题.(难点)1.通过对双曲线几何性质的学习,培养学生直观想象素养.2.借助于几何性的应用,提升学生的逻辑推理,数学运算素养.1.双曲线的几何性质标准方程-=1(a>0,b>0)-=1(a>0,b>0)性质图形焦点( - c, 0) , ( c, 0) (0 ,- c ) , (0 , c ) 焦距2 c 范围x ≤ - a 或 x ≥ a ,y∈Ry ≤ - a 或 y ≥ a ,x∈R性质对称性对称轴:坐标轴;对称中心:原点顶点A1( - a, 0) , A 2( a, 0) A1( 0 , - a ) , A 2( 0 , a ) 轴实轴:线段 A1A2,长:2 a ;虚轴:线段 B1B2,长:2 b ;实半轴长:a,虚半轴长:b离心率e=∈(1 ,+∞ ) 渐近线y = ± x y = ± x 思考 1:能否用 a,b 表示双曲线的离心率?[提示] e===.思考 2:离心率对双曲线开口大小有影响吗?满足什么对应关系?[提示] 有影响,因为 e===,故当的值越大,渐近线 y=x 的斜率越大,双曲线的开口越大,e 也越大,所以 e 反映了双曲线开口的大小,即双曲线的离心率越大,它的开口就越大.2.等轴双曲线实轴和虚轴相等的双曲线叫等轴双曲线,它的渐近线是 y = ± x ,离心率 e=.11.若 0