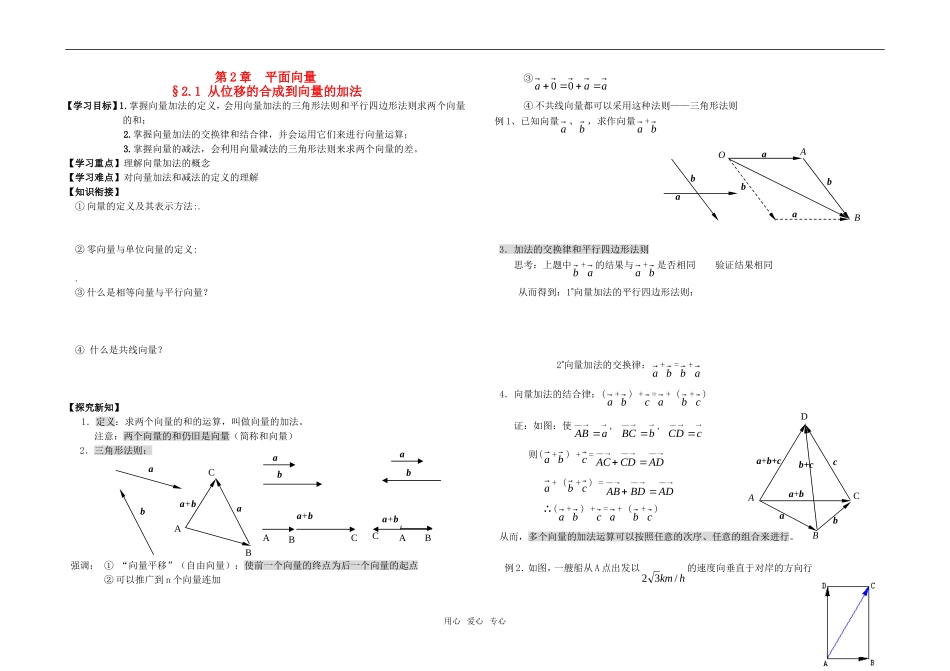
第 2 章 平面向量§2.1 从位移的合成到向量的加法【学习目标】1.掌握向量加法的定义,会用向量加法的三角形法则和平行四边形法则求两个向量的和; 2.掌握向量加法的交换律和结合律,并会运用它们来进行向量运算; 3.掌握向量的减法,会利用向量减法的三角形法则来求两个向量的差。【学习重点】理解向量加法的概念【学习难点】对向量加法和减法的定义的理解【知识衔接】① 向量的定义及其表示方法:.② 零向量与单位向量的定义:.③ 什么是相等向量与平行向量?④ 什么是共线向量?【探究新知】 1.定义:求两个向量的和的运算,叫做向量的加法。 注意:两个向量的和仍旧是向量(简称和向量) 2.三角形法则: 强调: ① “向量平移”(自由向量):使前一个向量的终点为后一个向量的起点 ② 可以推广到 n 个向量连加 ③aaa00 ④ 不共线向量都可以采用这种法则——三角形法则 例 1、已知向量a、b,求作向量a+b 3.加法的交换律和平行四边形法则思考:上题中b+a的结果与a+b是否相同 验证结果相同从而得到:1向量加法的平行四边形法则: 2向量加法的交换律:a+b=b+a4.向量加法的结合律:(a+b) +c=a+ (b+c)证:如图:使aAB, bBC, cCD则(a +b ) +c =ADCDAC a + (b +c ) =ADBDAB∴(a+b) +c=a+ (b+c)从而,多个向量的加法运算可以按照任意的次序、任意的组合来进行。例 2.如图,一艘船从 A 点出发以hkm /32的速度向垂直于对岸的方向行用心 爱心 专心a+bAAABBBCCCOABaaabbba+ba+baabbbaaABCDaca+b+cba+bb+c驶,同时水的流速为hkm/2,求船实际航行的速度的大小与方向。【巩固练习】【学后反思】【作业布置】1.如图,已知向量 a, b, c 不共线,求作向量 a+b+c。2.化简:用心 爱心 专心