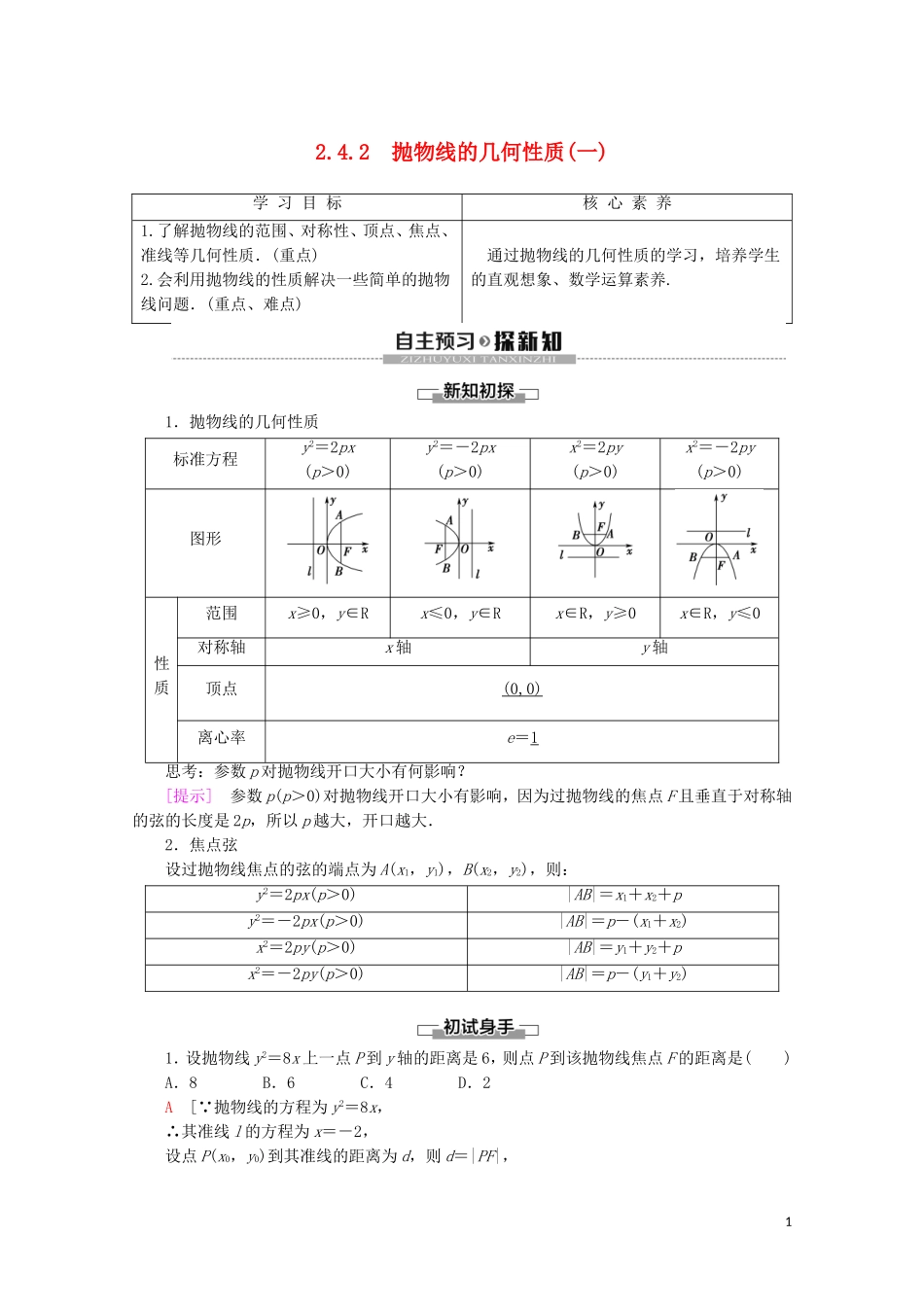
2.4.2 抛物线的几何性质(一)学 习 目 标核 心 素 养1.了解抛物线的范围、对称性、顶点、焦点、准线等几何性质.(重点)2.会利用抛物线的性质解决一些简单的抛物线问题.(重点、难点) 通过抛物线的几何性质的学习,培养学生的直观想象、数学运算素养.1.抛物线的几何性质标准方程y2=2px(p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0)图形性质范围x≥0,y∈Rx≤0,y∈Rx∈R,y≥0x∈R,y≤0对称轴x 轴y 轴顶点(0,0)离心率e=1思考:参数 p 对抛物线开口大小有何影响?[提示] 参数 p(p>0)对抛物线开口大小有影响,因为过抛物线的焦点 F 且垂直于对称轴的弦的长度是 2p,所以 p 越大,开口越大.2.焦点弦设过抛物线焦点的弦的端点为 A(x1,y1),B(x2,y2),则:y2=2px(p>0)|AB|=x1+x2+py2=-2px(p>0)|AB|=p-(x1+x2)x2=2py(p>0)|AB|=y1+y2+px2=-2py(p>0)|AB|=p-(y1+y2)1.设抛物线 y2=8x 上一点 P 到 y 轴的距离是 6,则点 P 到该抛物线焦点 F 的距离是( )A.8 B.6 C.4 D.2A [ 抛物线的方程为 y2=8x,∴其准线 l 的方程为 x=-2,设点 P(x0,y0)到其准线的距离为 d,则 d=|PF|,1即|PF|=d=x0-(-2)=x0+2, 点 P 到 y 轴的距离是 6,∴x0=6,∴|PF|=6+2=8.]2.顶点在原点,对称轴为 y 轴,顶点到准线的距离为 4 的抛物线方程是 ( )A.x2=16y B.x2=8yC.x2=±8y D.x2=±16yD [顶点在原点,对称轴为 y 轴的抛物线方程有两个:x2=-2py,x2=2py(p>0).由顶点到准线的距离为 4 知 p=8,故所求抛物线方程为 x2=16y,x2=-16y.]3.已知抛物线 y2=2px(p>0)的焦点 F,点 P1(x1,y1)、P2(x2,y2)、P3(x3,y3)在抛物线上,且2x2=x1+x3,则有( )A.|FP1|+|FP2|=|FP3|B.|FP1|2+|FP2|2=|FP3|2C.|FP1|+|FP3|=2|FP2|D.|FP1|·|FP3|=|FP2|2C [由抛物线定义知|FP1|=x1+,|FP2|=x2+,|FP3|=x3+,∴|FP1|+|FP3|=2|FP2|,故选 C.]由抛物线的几何性质求标准方程【例 1】 抛物线的顶点在原点,对称轴重合于椭圆 9x2+4y2=36 短轴所在的直线,抛物线焦点到顶点的距离为 3,求抛物线的方程及抛物线的准线方程.[思路探究] 解答本题可先确定椭圆的短轴,从而确定抛物线的焦点位置,再写出标准方程即可.[解] 椭圆的方程可化为+=1,其短轴在 x 轴上,∴抛物线的对称轴为 x 轴,∴设抛物线的方程为 y2=2px ...